Problema 645
Sea ![]() un triángulo equilátero. Sea O el circuncentro.
un triángulo equilátero. Sea O el circuncentro.
Sea M en el lado ![]() , N en el lado
, N en el lado ![]() tal que
tal que ![]() .
.
Probar que el perímetro del triángulo ![]() es igual al lado del triángulo equilátero.
es igual al lado del triángulo equilátero.
Peiró, R. (2012): Comunicación personal.
Solución del director:
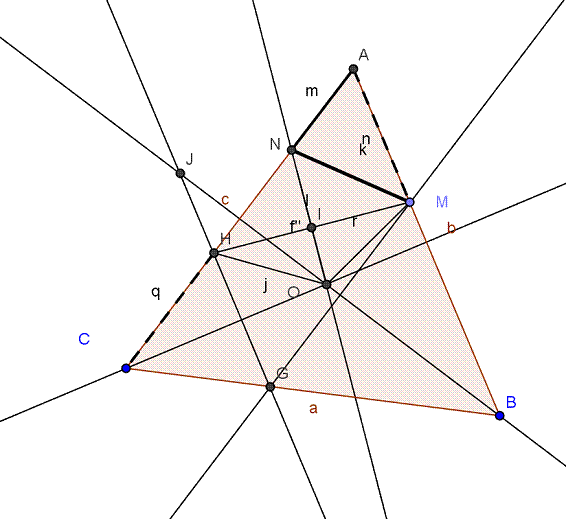
Sea MG paralela a AC con G sobre CB. CG=AM, por ser BMG equilátero (por ejemplo, es una de las posibles demostraciones de esta propiedad…)
Así, trazando GH paralela a BA con H sobre AC, es CH=CG=AH.
Luego hemos de ver que MN=HN.
Es OH=OG =OM por ser HG paralela a AB y ser OHG y OMG isósceles.
Así, los triángulos OMN y OHN tienen un lado igual y un lado común.
Por otra parte, si giramos OMA 120º con centro en O , obtenemos el triángulo OHC.
Así <MOH=120º, y como <MON=60º, es NOH=60º, y de ello los triángulos OMN y OHN son congruentes, por lo que MN=HN.
Así, AN +NM+MA= AN+NH + HC=AC, cqd
Ricardo Barroso Campos
Didáctica de las Matemáticas
Universidad de Sevilla.