Problema 646

A) Let G₁ be the triangle formed by the feet of the perpendiculars from P on the sides of the triangle G. Form G ₂ from G₁ and P in the same way. Likewise construct G ₃ from G₂ and P. Then the triangle G₃ so constructed is necessarily similar to the original triangle G.

Sea G₁ el triángulo que forman los pies de las perpendiculares trazadas desde P a los lados del triángulo G.

Construimos G ₂ a partir de G₁ y P de la misma manera. Igual G ₃ a partir de G₂ y P.

Entonces el triángulo G₃ es necesariamente semejante al triángulo original G.

El punto P es del plano y no está sobre los lados de G.

OPPENHEIM, A. (1961): THE ERDOS INEQUALITY AND OTHER INEQUALITIES FOR A TRIANGLE. The American Mathematical Monthly, Vol. 68, No. 3 (Mar., 1961), pp. 226-230.

Solución del apartado A) del director:

Supongamos P interior a ABC

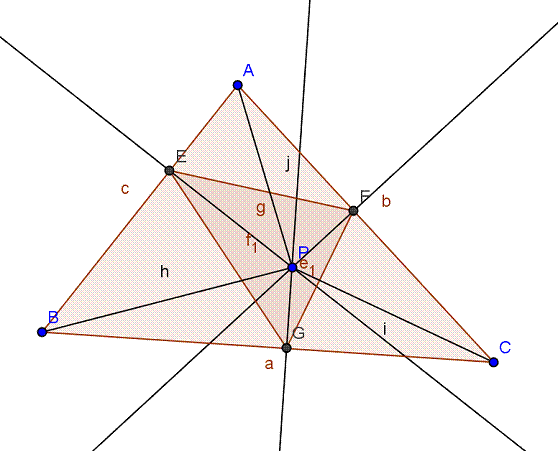
Sea ‹PBA= α,  ‹PBC= β, ‹PCB= γ, ‹PCA= θ, <PAC=Λ, ‹PAB= ω.

ES:   ‹PEG= β,  ‹PGE= α, ‹PGF= θ, ‹PFG= γ, <PFE=ω, ‹PEF= Λ.

Por ser PGBE, PGCF y PFAE cuadriláteros concíclicos.

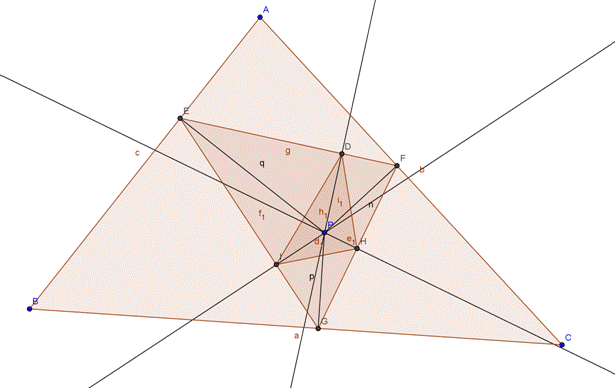
Sea G₂  HDI . Por razones similares tenemos:

   ‹PEG= β,  ‹PGE= α, ‹PGF= θ, ‹PFG= γ, <PFE=ω, ‹PEF= Λ.

ES:   ‹PIH= θ,  ‹PHI= α, ‹PID= Λ, ‹PDI= β, <PHD=ω, ‹PDH=γ.

ES:   ‹PIH= θ,  ‹PHI= α, ‹PID= Λ, ‹PDI= β, <PHD=ω, ‹PDH=γ.

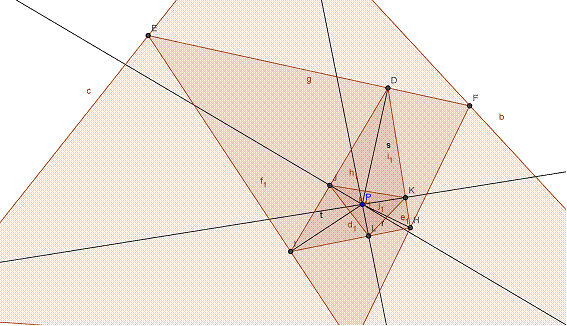
Por último de manera análoga, en G₃, tenemos:

ES:   ‹PKJ= β,  ‹PJK= γ, ‹PLJ= Λ, ‹PJL= θ, <PLK=ω, ‹PKL=α.

Luego :     ‹JKL= α+β=<ABC, ‹LJK= γ+θ=ACB , ‹KLJ= ω +Λ=<BAC.

Así pues, son semejantes, cqd

Caso de ser P exterior por ejemplo en la amplitud de B, y el semiplano que no lo contiene  a B.

 

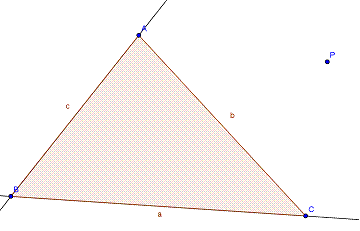
Tracemos PA, PB y PC y  G₁, DEF, triángulo pedal de ABC respecto a P

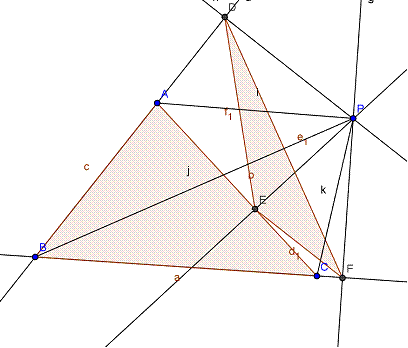
Sean: ‹PBA= α,  ‹PBC= β, ‹PAD= γ, ‹PAC= θ, <PCA=Λ, ‹PCF= ω.

Es por ser concíclicos los respectivos cuadriláteros:

‹PFD= α,  ‹PDF= β, ‹PEF= ω, ‹PED=γ,

<PFE=Λ, (por lo que  <DFE=Λ-α), ‹PDF= θ  (por lo que <EDF=θ-β).

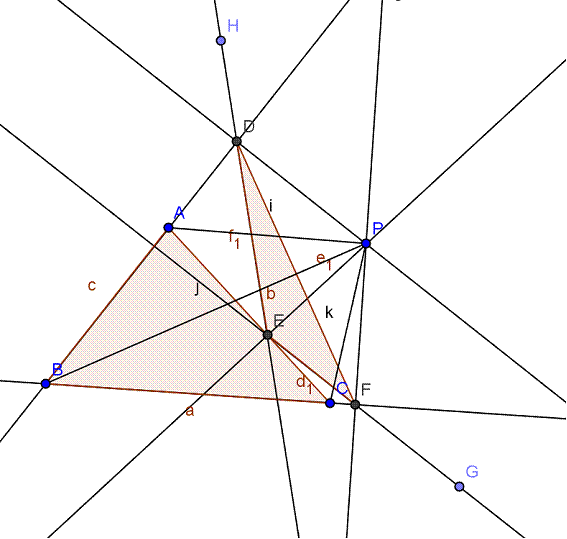
Así considerando las prolongaciones de EF , EFG y de ED, EDH, tenemos que :

‹PFD= α,  ‹PDF= β, ‹PEF= ω, ‹PED=γ,  <PFG=180-Λ, ‹PDH=180- θ .

Tracemos ahora G₂, IJL, con I sobre DE, J sobre DF y L sobre EF

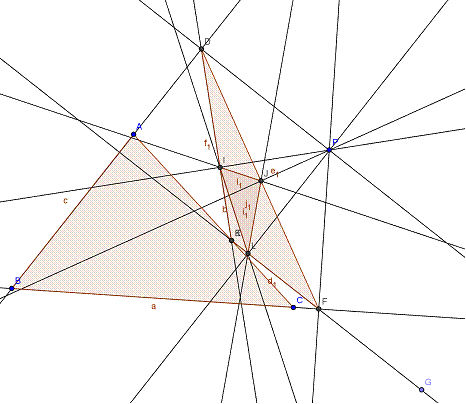
Tenemos: <PJI=180- θ al ser concíclico PJID. <PJL=180-Λ al ser PJLF concíclico.

<PLJ=α, y <PIJ=β.

Sean R y S sobre las prolongaciones de IL, en sentido RILS (que RS no aparecen en la figura).

<PIR=180-ω, <PLS=180-γ.

Ampliemos la figura para generar G₃, 

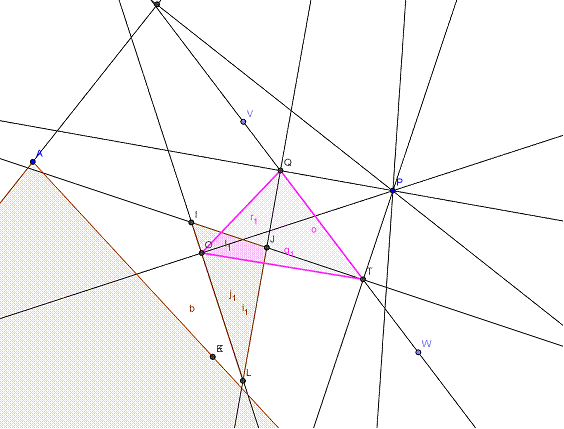
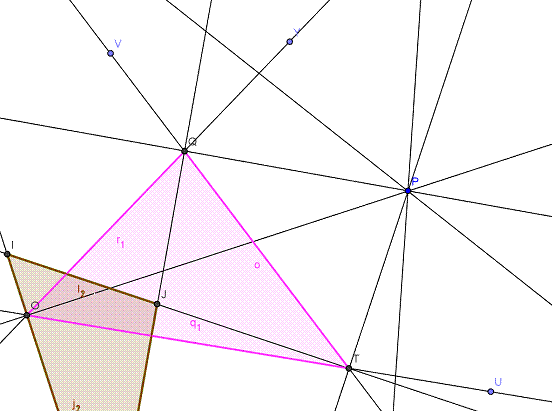
 Tenemos que considerar OQT.

Análogamente a lo hecho anteriormente, es:

<POQ= <PLQ=<PLJ=α, <POT=<PIT=<PIJ=β

<PQT=<PJT=180-PJI=180-(180-θ)=θ. <PTQ=<PJQ=180-PJL=180-(180-ω)=ω.

Prolonguemos OTU y OQY:

Por analogía de las estructuras estudiadas, es

<PTU=180-<PFD= 180- (180-Λ)=Λ.

<PQY=180- <PLS=180-(180-γ)=γ.

Así, <QOT=α+β=<ABC.

<OQT=180-<YQT=180-<YQP-<TQP=180-γ-θ=<BAC.

<OTQ=180-<UTQ=180- <UTP-<PTQ=180- Λ- ω= <ACB.

Es decir, cqd, ABC y G3 son semejantes.