Problema 646.- A) Sea T₁ el triángulo que forman los pies de las perpendiculares trazadas desde P a los lados del triángulo G.

Construimos T₂ a partir de T₁ y P de la misma manera. Igual T₃ a partir de T₂ y P.

Entonces el triángulo T₃ es necesariamente semejante al triángulo original T.

El punto P es del plano y no está sobre los lados de T.

B) Hallar los puntos P para los que T y T₃  son homotéticos con centro de homotecia P. ¿En qué casos es la homotecia directa y en cuales inversa?

Solución de la primera parte de Saturnino Campo Ruiz, profesor de Salamanca.

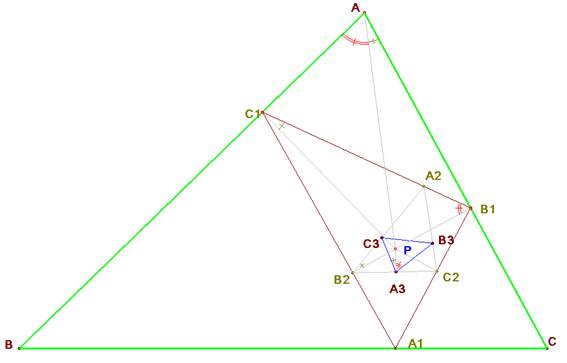
A) En la figura se observa que los cuadriláteros siguientes son cíclicos o inscriptibles:

AB1PC1;  A₂B₁C₂P;  A₃C2B₃P; A2C1B2P  y A₃B2C₃P.

De ello se deducen las relaciones angulares siguientes:

de otra parte

Por tanto,  pues las dos partes en que se dividen por los segmentos que los unen con P se corresponden.

Análogamente, obtenemos que   y

Por lo tanto, los triángulos ABC y A₃ B₃ C₃ son semejantes. Y con esto queda probada la parte A) del problema.

B) De los puntos P cuyo tercer triángulo pedal es homotético al primero, con centro de homotecia P, destacamos el ortocentro, el incentro y excentros del triángulo así como el circuncentro. En general, el primer triángulo pedal trazado desde el circuncentro es el triángulo medial. Esto lo usaremos varias veces más adelante.

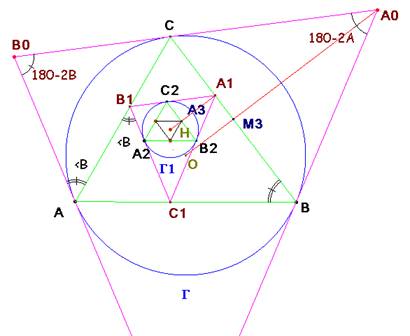
Veamos que el ortocentro es uno de estos puntos. En efecto: Construimos el triángulo  tangencial de T=ABC.   El triángulo pedal de T a partir del ortocentro H es el triángulo órtico , en tanto que T es el triángulo pedal de  a partir del circuncentro O.

Los triángulos tangencial  y órtico tienen sus lados paralelos.  En efecto, basta hacer un cómputo de ángulos para verlo.

de donde se sigue que , e igualmente con los demás lados. En consecuencia, son homotéticos.

En esa homotecia entre   y se corresponden las circunferencias inscritas, los centros de ellas, los triángulos pedales…  etc., por tanto, triángulo pedal de (respecto de O) es homotético con , triángulo pedal de  (respecto de H).  es el triángulo pedal (y medial)  de por tanto es perpendicular a  y a ; también la altura es perpendicular a . Luego A, H y   están alineados.

En el caso del incentro y los excentros como el I es el centro de la circunscrita a , resulta que  es su triángulo medial.

La bisectriz AI es también la mediatriz del triángulo isósceles . AI es perpendicular a  y a pues estos segmentos son paralelos. El punto de encuentro con éste último es el vértice A₃. Por tanto A y A₃ están alineados con I. Los triángulos son homotéticos.

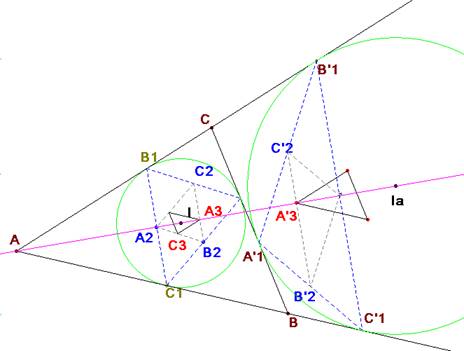
Para el excentro  la situación es similar:  (semiperímetro de ABC). La bisectriz  es mediatriz de . Del mismo razonamiento de antes para la circunferencia de centro  resulta que A y están alineados con , sin más que cambiar en los segmentos los vértices  por .

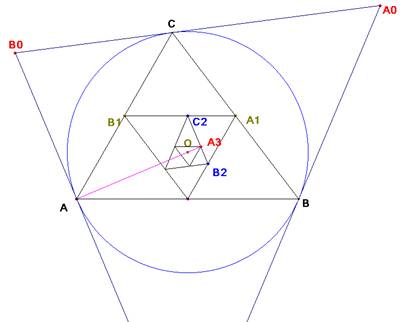Ahora el  circuncentro O: Seguiremos llamando  a los triángulos pedales de T respecto de O, aunque no coincidan con los anteriores, solamente  tangencial de T=ABC son iguales.

El circuncentro es el incentro del triángulo tangencial . Por tanto, O es el centro de la homotecia de este triángulo con  (el tercer triángulo pedal del ). En consecuencia , paralelo a , es perpendicular a OA.

Por construcción  es perpendicular a , (y a ) y por tanto, los puntos O, A y   están alineados, como queríamos probar.

Las homotecias son directas cuando P es exterior, inversas en caso contrario.