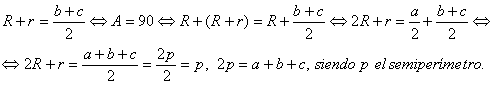Problema 647
14. En un triángulo rectángulo, el semiperímetro es igual a la suma de radio del círculo inscrito y del diámetro del círculo circunscrito (esto es evidente). Demostrar que recíprocamente, si en un triángulo el semiperímetro es igual a la suma del radio del círculo inscrito y del diámetro del círculo circunscrito, el triángulo es rectángulo.
Lemoine, E. (1900): El progreso Matemático. Zaragoza, 20 de Septiembre de 1891. Año I, n . 9º. Pág 240)
Solución de Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid.
En AMM, aparece propuesto y resuelto, respectivamente, en Vol.106, N.2. (Feb., 1999) , p.166. y Vol.107, N.5. (May, 2000), p.464, el Problema 10713 , al cual el editor de la revista le dio el título:
A Cute Characterization of Acute Triangles
Sea dado un triángulo con ángulos 
y sean a,b, y c las longitudes de los lados correspondiendo a los lados opuestos, sean r y R, los radios del círculo inscrito y circunscrito respectivamente. Demostrar que A es un ángulo agudo si y sólo si R+r < (b+c)/2.
Presentamos la solución publicada debida a Heinz-Jurgen Seiffert.
La condición 
puede sustituirse por la condición más débil 
Por el Teorema de los senos R sabemos que 2R = a/Sen A = b/ Sen B = c/ Sen C, y como
implica
El radio r del círculo inscrito se puede escribir después de operar adecuadamente así :
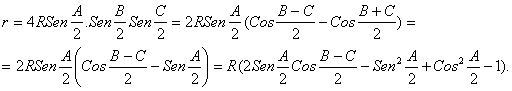
De todo lo anterior, tenemos que
Pero
y por tanto tenemos que
La condición 
implica que 
por tanto que el factor del segundo miembro es positivo. De ello seguimos que R+r- (b+c)/2 < 0 si y solo si Sen(A/2) <Cos(A/2), que es cierto siempre que el ángulo A sea un ángulo agudo.
Podemos entonces, un nuevo problema que relaciona el Problema de Erdos, y los problemas de AMM, 10713, y 11055, como sigue :
Sea ABC un triángulo no obtusángulo cuyos lados verifican que 
Si h es la mayor altura del triángulo y r, R son el radio del círculo inscrito y el radio del círculo circunscrito, respectivamente, probar que :
Posteriormente, en Crux, se generalizó este problema con el número 2690, en la forma siguiente :
Sea ABC un triángulo con ángulo mayor A del lado mayor. Sea r y R el radio del círculo inscrito y del círculo circunscrito, respectivamente.
Probar que
La solución que se publica es también la de Heinz-Jurgen Seiffert, que hace mención al problema anterior.
Notas.
a) Este problema tiene varios antecedentes muy antiguos, Lemoine, en el Progreso Matemático, primera serie, como cuestión 267, que quedó pendiente de resolver, y más tarde se propuso y se resolvió para el caso de triángulos rectángulos, en la segunda serie en que comenzó a editarse de nuevo esta revista, y apareció resuelto.
b)Más recientemente, aparece los siguientes antecedentes del mismo, en la revista Crux Mathematicorum, a saber :
Volume 15 # 9, November, 1989, en
Prove that in any acute triangle, the sumo f circumradius and the inradius is less that length of the second-longest side.
Se dan dos soluciones que aparecen en Crux, Volume 17 # 1, January, 1991, en la sección de problemas , pp. 26-27. Una de las soluciones es geométrico debida al Prof. Toshio Seimiya, y otra solución que es trigonométrica debida al proponente que bajo la hipótesis 
prueba que 
Solución al problema 647.
Este problema por la parte correspondiente para triángulos rectángulos del problema
2690 es equivalente al siguiente:
