Problema 647.- En un triángulo obtusángulo, el semiperímetro es menor que la suma del radio del círculo inscrito y del diámetro del círculo circunscrito.
Barroso, R (2012). Comunicación personal.
Solución de Saturnino Campo Ruiz, profesor de Matemáticas de Salamanca.
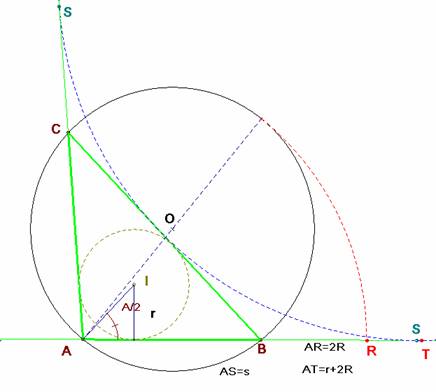
Suponiendo que el ángulo A sea obtuso se tienen las siguientes expresiones para los radios:
![]() y
y ![]() . Se pretende demostrar que
. Se pretende demostrar que
![]()
![]() (1)
(1)
Como 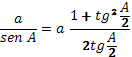 , sustituyendo en (1) se tiene para el segundo miembro
, sustituyendo en (1) se tiene para el segundo miembro
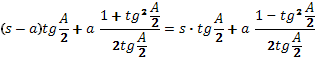
La expresión (1) equivale a
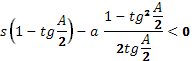 (2)
(2)
En la hipótesis del triángulo obtusángulo ![]() , por tanto, en la desigualdad anterior, simplificando el término
, por tanto, en la desigualdad anterior, simplificando el término ![]() , se tiene
, se tiene
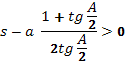 (3)
(3)
Operando se obtiene ![]() , o bien
, o bien ![]() , lo cual es evidente, al ser obtuso el ángulo A.
, lo cual es evidente, al ser obtuso el ángulo A.
![]()