Propuesto por Juan Bosco  Romero  Márquez, profesor colaborador de la Universidad de Valladolid.

Problema 648.-  Sea AD una ceviana arbitraria para el triángulo ABC, donde D es su pie sobre BC y que divide al triángulo en los triángulos ADB y ADC. Sean DF y DI las bisectrices interiores del ángulo D en los triángulos ADB y ADC, donde F e I están sobre AB y AC respectivamente. Construimos los rombos DEFG y DHIJ, sobre los triángulos ADB y ADC respectivamente, donde G y J están sobre AD.

Definimos además los puntos K=AC·EF, L=AB·IH, M=DK·AB y N=DL·AC.

Probar que:

a) AD, IM y FM se cortan en un punto que denotamos por X.

b) Lugar geométrico de X cuando D varía sobre BC.

Romero, J.B. (2012). Comunicación personal.

Solución de la primera parte de Saturnino Campo Ruiz, de Salamanca.

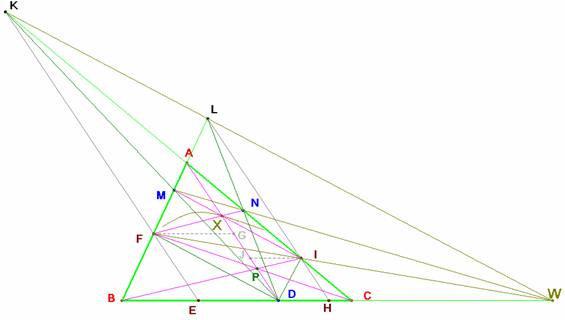
En primer lugar observamos que de los rombos que se añaden a la figura, los puntos G y J no cumplen ninguna función. En realidad bastaría con decir que se trazan por I y F rectas paralelas a la ceviana AD. Incluso esta condición podría sustituirse por una más general: desde un punto V sobre la ceviana AD se proyectan los puntos I y F sobre los lados c, b del triángulo (el enunciado toma V en el infinito). Además I y F se hacen depender de D, y para esta primera parte pueden considerarse como puntos arbitrarios sobre las rectas .

Podemos, pues, tomar el siguiente enunciado que generaliza el original:

Sean tres rectas a, b y c del haz de rectas que pasan por un punto A del plano. Sean V y D dos puntos diferentes sobre a, I sobre b y F sobre c; L y K las proyecciones de I y F desde V sobre c y b respectivamente; N y M las proyecciones de L y K desde D sobre b y c.

Probar que las rectas FN, IM se cortan en un punto X que también pertenece a AD.

Por último: las rectas FI, MN y KL concurren en un punto W.

 

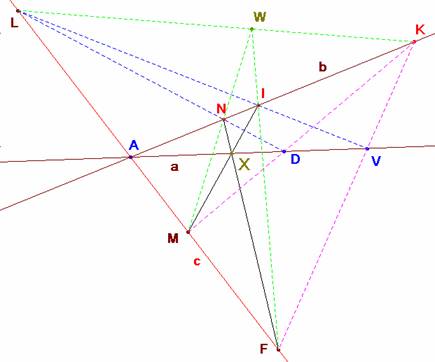
La proyectividad definida entre las rectas b y c en la que se corresponden

es una perspectividad  (pues el punto común A es doble) de eje la recta a=AD. Si llamamos X al punto de intersección de la recta definida por I y M con la definida por N y F, este punto ha de pertenecer al eje de dicha proyectividad: la recta a=AD, con lo que se demuestra lo solicitado en el apartado a) del problema.

Además, al tratarse de una perspectividad, todas las rectas definidas mediante un punto y su homólogo concurren en un punto W, que se llama centro de la perspectividad.

En el planteamiento inicial del problema, los puntos A y B se corresponden en esa perspectividad y también están alineados con W.

Bastará demostrar que las rectas  son concurrentes.

Según el teorema de la bisectriz  y ,  por tanto, si ahora aplicamos el teorema de Ceva se obtiene  =1, que demuestra la concurrencia. Así pues .

El homólogo de B en esa perspectividad puede obtenerse uniéndolo con I.  corta al eje de la misma (recta ) en . La proyección de P desde F (homólogo de I) sobre b=AC es, según la concurrencia anterior, el punto C. Por tanto B y C también están alineados con W.