Propuesto por Ramón Trigueros Reina, profesor Asociado Doctor del Departamento de Didáctica de las Matemáticas de la Universidad de Sevilla y del IES Triana de Sevilla, y el director de Trianguloscabri.
Problema 651
Dado un triángulo ABC, encontrar el lugar geométrico de los puntos P tales que
las áreas [PAB], [PAC] y [PBC], tomadas en valor absoluto, y en cualquier orden sean una progresión geométrica.
Trigueros, R. y Barroso, R. (2012): Comunicación personal.
Solución del director:
Tomemos sin pérdida de generalidad coordenadas cartesianas.
A(0,0), B(b,0), C(c,d).
Sea P (x,y).
Tenemos:
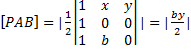
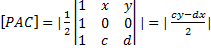
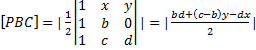
Tenemos varias opciones:
Supongamos que la progresión geométrica sea de razón r, con
[PAB], [PAC]=[PAB]r, [PBC]=[PAB]r2.
Tendríamos [PBC]
[PAB]=[PAC]2
![]()
Lo
que da lugar a una ecuación general de segundo grado, que es una cónica.
Concretemos valores en esta fase.
Supongamos que el triángulo fuese A(0,0), B(6,0), C(4,7).
![]()
Hay dos posibilidades:
a) Supongamos que 42>2y+7x:
![]() ,
,
Es
decir:
![]()
O sea ,
![]()
0
bien
![]()
Se
trata de una elipse, por ser
(-2)2
– 4 (4) (7)=-108 <0
que contiene a A (0,0) y C
(4,7), al baricentro G(3 1/3, 2 1/3), al
punto B`(-2,7) simétrico de
B(6,0) respecto al punto medio
de AC, Mb(2,3 ½).
Hallemos
las tangentes a la elipse en A y C:
8y
y’ -2y – 2xy’ +14x - 36y’=0,
De
donde![]()
Para
A(0,0) es y’(0,0)=0, luego la tangente a la elipse en
A(0,0) es y-0=0(x-0), o sea y=0, que es la recta del lado AB.
Para C(4,7),
![]()
Luego
la tangente en C a la elipse es![]()
Es
la recta del lado BC.
Por
otra parte la pendiente de la tangente en el baricentro de la elipse
![]()
es
![]() .
.
La
pendiente de la tangente a
![]()
en el punto B`(-2,7)
es:
![]() .
.
Y
por tanto ambas tangentes son paralelas, lo que indica que GB’ es un diámetro
de la elipse.
Así
el centro de la elipse es su punto medio, U(2/3, 14/3)
a) Supongamos que 42<2y+7x:
![]() ,
,
Es
decir:
![]()
O sea ,
![]()
Se
tiene 982- 4 (-4) (-49)=8820>0, por lo que esta ecuación es una
hipérbola.
Esta
hipérbola contiene a los vértices A(0,0), y C(4,7),
así como a los simétricos de A (0,0) respecto al punto medio Ma(5,3.5) de BC , que es A’(10,7), como al de
C(4,7) respecto al punto medio Mc (3,0) de AB, C’(2,-7)
La
pendiente en un punto de la hipérbola es:
![]()
Es
decir:![]()
Así
en A(0,0) es ![]()
Y la
recta tangente en A (0,0) es y-0=0(x-0), y=0.
O
sea la hipérbola es tangente a la recta AB.
En
el punto C la pendiente de la recta tangente a la hipérbola es:
r:![]()
Así
la recta tangente a la hipérbola en C(4,7) es
(![]()
Por
lo que la hipérbola es tangente a la recta CB.
De
manera análoga se construyen otras dos elipses y otras dos hipérbolas.
12805.33333x²
- 3658.66667x y + 7317.33333y² - 76832x + 43904y = 0
20744.64x²
- 5927.04x y - 18627.84y² - 124467.84x + 71124.48y = 0
1600.66667x²
- 457.33333x y + 914.66667y² - 19208x - 5488y = -57624
2074.464x²
+ 2963.52x y - 846.72y² - 24893.568x - 7112.448y = -74680.704
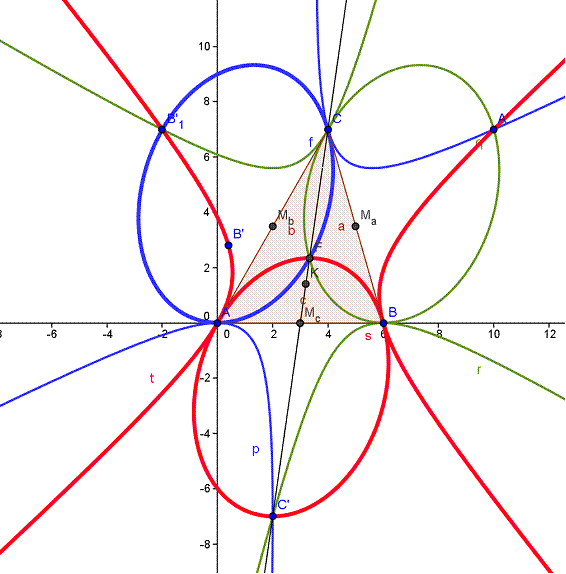
Imagen
tomada de Geogebra
Ricardo
Barroso Campos.
Didáctica
de las Matemáticas.
Universidad
de Sevilla.