Propuesto por el director

Problema 655

Construir un triángulo ABC con inradio r y circunradio R tal que tenga una única circunferencia tangente interiormente a la circunferencia circunscrita y a la vez sea tangente exteriormente a la circunferencia inscrita, que tenga radio r.

Barroso, R. (2012): Comunicación personal.

Solución del director

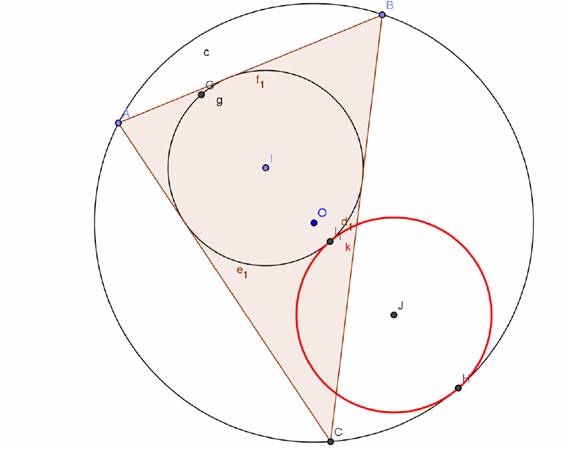
El lugar geométrico de los centros de las circunferencias tangentes a la inscrita y a la circunscita es una elipse de focos el incentro I y circuncentro O y de suma de radios vectores r+ R.

Sea d=|IO|

La cirunferencia pedida ha de estar en la recta IO. El radio máximo es (R-r+d)/2.

Debe ser  (R-r+d)/2=r luego R+d=3r.

Por Euler, tenemos R² –d²=2rR.

Luego R-d=(2/3) R, d=(1/3) R

Así es r=(R+d)/3=(4/9)R.

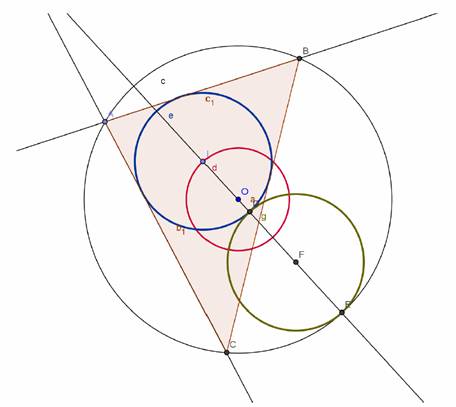
Se ala circunferência de centro O y radio R.

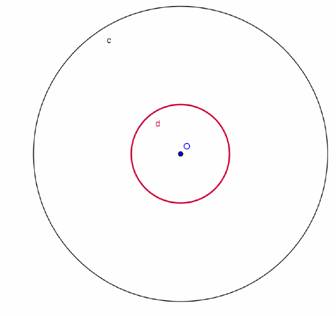
Circunferencia  d de centro O y radio R/3. Em ella há de estar el incentro I

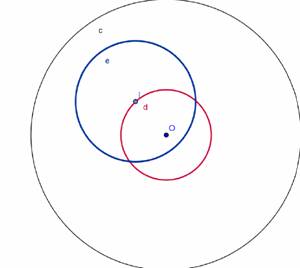
La circunferencia de e de centro I y radio (4/9) R es la inscrita de ABC.

Sea A sobre la circunferencia c. Sean AB y AC tangentes a la circunferencia e, con B y  C sobre c.

ABC es una solución.

Ricardo Barroso Campos.

Didáctica de las Matemáticas.

Universidad de Sevilla.