Problema 657.

Sea ABC un triángulo. Construyamos sobre la recta BC los puntos T y U tal que <ATC=<BAC y <AUB=<BAC. Se tiene AB²+AC ²= BC (UB+TC). (Este resultado es conocido como generalización de Thabit del teorema de Pitágoras)

De Villiers, M. (1994-2009) : Some adventures in Euclidean Geometry.

Solución del director

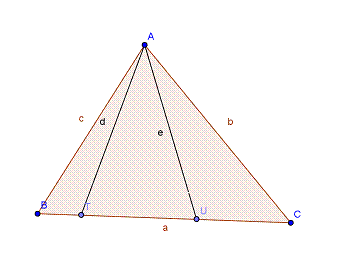
Δ AUB ΔCAB por lo que AB/UB = CB/AB y así AB²=CB UB

Δ ATC ΔBAC por lo que AC/TC = BC/AC y así AC²=BC TC

Se tiene AB²+AC ²= BC (UB+TC).

Si A es ángulo recto, U=T, y tenemos el teorema de Pitágoras

Ricardo Barroso Campos

Didáctica de las Matemáticas.

Universidad de Sevilla