Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid.

Problema 658. - Sea ABC un triángulo. Los puntos A_bi, A_ci, A_br,A_cr,están sobre la recta BC tales que AB=BA_bi , con A_bi en el lado opuesto a C, AC=CA_ci , con  A_ci en el lado opuesto a B, y los triángulos ABA_br y ACA_cr rectángulos en A.

Sea r la recta paralela a AC que pasa por A_bi.

Sea s la recta paralela a AB que pasa por A_ci.

Sea A’ la intersección de r y s. Sea B’ la intersección de s y la recta AA_cr . Sea C’ la intersección der y la recta AA_br .

Sea D la intersección de las las rectas AA’ y B’C’. Sea E la intersección de las las rectas s y AC’.

Sea F la intersección de las rectas r  y AB’.

Demostrar que el triángulo EDF es el órtico del A’B’C’.

Romero, J.B. (2012). Comunicación personal.

Solución de Saturnino Campo Ruiz, Salamanca.

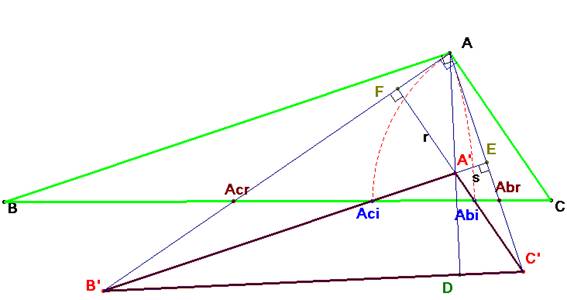
Es fácil ver, según la construcción realizada, que  y  son alturas del triángulo . Por tanto  es la otra altura, y en consecuencia  es el triángulo órtico de  como se pretendía demostrar. Su ortocentro es el punto .