Un lado de un triángulo, la bisectriz y la altura que parten de un vértice, miden 17, 10 y 8cm.

Calcular el área del triángulo.

Resolver el triángulo conocidos el lado , la altura y la bisectriz .

Calcular el área.

Problemas de estado. Edelvives.

Solución de Ricard Peiró:

Es conveniente dibujar el problema con regla y compás

Para ver que la solución es única y además C es obtusángulo.

Figura barroso660.fig

Siga , .

Siga .

Aplicando el teorema de Pitágoras al triángulo rectángulo :

.

Aplicando el teorema de Pitágoras al triángulo rectángulo :

.

, .

Aplicando la propiedad de la bisectriz:

(1)

Aplicando el teorema de Pitágoras al triángulo rectángulo :

(2)

Consideremos el sistema formado por las expresiones (1) (2):

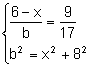. Resolviendo el sistema: .

.

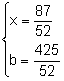El área del triángulo es:

.

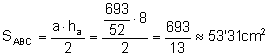Acabaremos resolviendo el triángulo.

. .

Aplicando el teorema de los senos al triángulo

. .

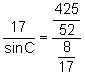C es obtuso ya que .

.

.

Nota: Construcción con regla y compás.

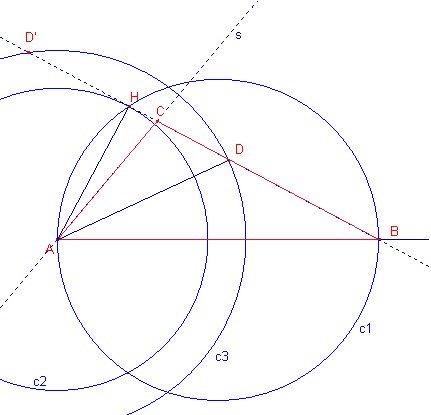
a) Dibujar el segmento .

b) Dibujar la circunferencia c1 de diámetro .

c) Dibujar la circunferencia c2 de centro A y radio .

d) Las circunferencias c1, c2 se cortan en H pie de la altura referida al lado a.

e) Dibujar la recta BH.

f) Dibujar la circunferencia c3 de centro A y radio .

g) La circunferencia c3 corta la recta BH en los puntos D, D’.

h) Dibujar la recta s simétrica de AB respecto de AD.

i) La recta s corta la recta BH en el punto C.

j) Notemos que entonces AD’ no puede ser bisectriz.