Problema 661
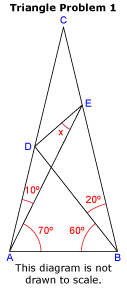
Sea ABC un triángulo tal que
1) D esté sobre el lado AC tal que < DBA=60º, <CBD=20º
2) E esté sobre el lado BC tal que <EAB=70º, <CAE=10º.
Hallar la medida del ángulo DEA.

http://thinkzone.wlonk.com/MathFun/Triangle.htm

Solución del director.
Tracemos la circunferencia Ω  de centro B y radio BA. Sea F la intersección de Ω con AC.
El triángulo AFB es isósceles por lo que <AFB=80. Tracemos la bisectriz de BFC, que cortará a Ω en G.  El triángulo BFG es isósceles por lo que tiene 80º, 50º, 50º.
Sea U el punto de corte de  FG con BD.

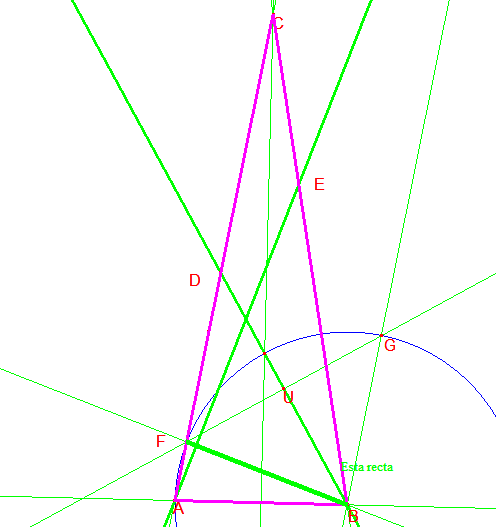
Veamos que FG es mediatriz de BD, pues
1) <FBU=<ABU-<FBU=60º - 20º = 40º.
2) <UFG=<BFG=50º
Por 1) y 2), en el triángulo BUF, es <BUF=90º 
Por otra parte, es
3)<BGU=<BGF=50º,
4)<BUG=90º
Luego de 3) y 4), en el triángulo BUG, es UBG=40º.
A continuación tenemos que
5)<UDF=<BDA= 180º- <BAD-<DBA=180º - 80º - 60º=40º
6)<UFB= 50º, por ser FU bisectriz del ángulo BFD.
De todo lo anterior se deduce que UD=UB y UG=UF, siendo perpendiculares FG y DB, por lo que cqd, FG es la mediatriz de BD.

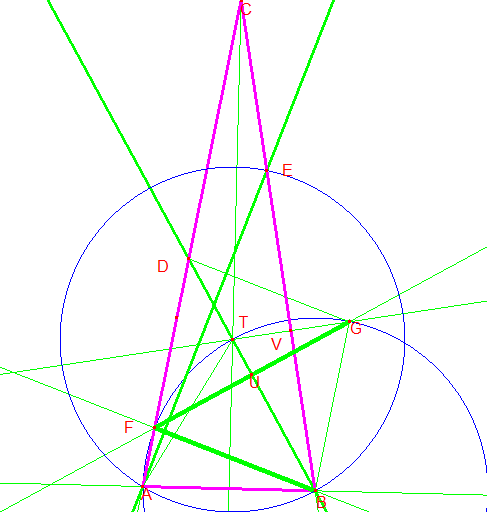
Sea ahora T el punto de corte de Ω con BD.
El triángulo TBG es isósceles, 70º,40º, 70º.
Además BTA es equilátero pues <TBA=<DBA=60º por construcción.
Al ser <AEB=180º-<EAB-<EBA=180º-80º-70º=30º, T es el centro de la circunferencia circunscrita al triángulo ABE.
Así el triángulo AET es isósceles y <TEA=<TAE=10º.
Por ello <TEV=<AEB-<AET=30º-10º=20º.
En definitiva el cuadrilátero ETBG es un rombo.
Así GT es perpendicular a EB, y es su mediatriz.

De lo expuesto se deduce que G es el  centro de la circunscrita a DBE.

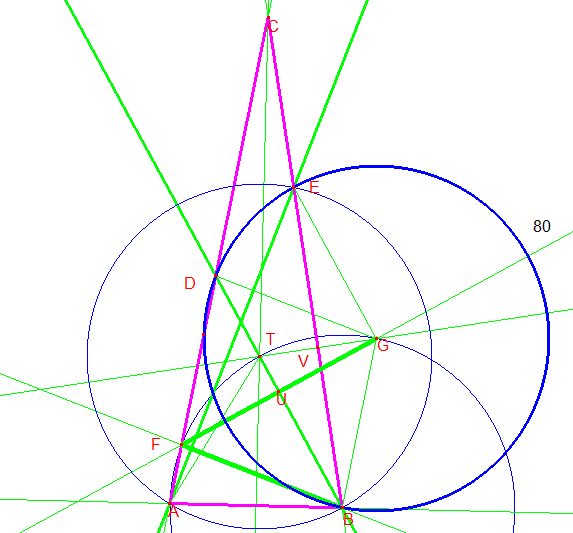
Además tiene de radio la longitud del lado AB.
<EGB=180º-<GBE-<GEB=180º-20º-20º=140º (convexo)
<EGB=360º-<EGB=360º-140º=220º (cóncavo)
Así el ángulo inscrito <EDB=110º.
Dado que <DEB=20º, es <DBE=180º-<DEB-<EDB=180º-20º-110º=50º.
Luego finlmente <DEA=<DEB-<AEB=50º-30º=20º.
Ricardo Barroso Campos.
Jubilado.