Problema 663.-
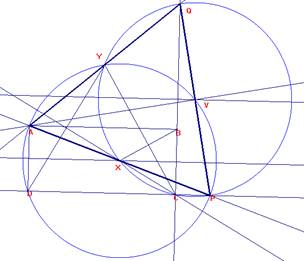
1.- Sea ABC D un rectángulo. Se construyen triángulos equiláteros BC X y DC Y de modo que estos triángulos comparten algunos de sus puntos interiores con los puntos interiores del rectángulo. Las rectas AX y C D se cortan en P , y las rectas AY y BC se cortan en Q. Probar que el triángulo AP Q es equilátero.
XXVII Olimpiada Iberoamericana de Matemáticas Cochabamba (BOLIVIA),2012)
Tomado de Matetam
Primera solución del director.
Comencemos observando el cuadrilátero AYPD.
La mediatriz de AD contiene a X.
La recta CX es la mediatriz de DY.
Así AYPD es inscriptible en la circunferencia de centro X y radio XA.
Por
tanto <QAP=<YAP=<YDP=60º.Es <BAD=α, luego <QAB=60º-α, y <BQA=30+α.
Tracemos por Q la perpendicular a AP; sea R el punto de corte de ambas.
En el triángulo ARQ será < QAR=60º, <ARQ= 90º=<PRQ, y <RQA=30º.
De esta manera el cuadrilátero PCRQ es inscriptible.
Además por ello, <CQR=<BQA-<RQA= 30º+α- 30º=α =<XPC.
Al ser X y R de AP, han de ser el mismo punto.
De todo ello, se tiene: <PQC=<XPC=180º-<XPC-<PCX=180º-α-150º=30º-α.
Así, tenemos <AQP=<AQC+<CQP=(30+α)+(30-α)=60º.
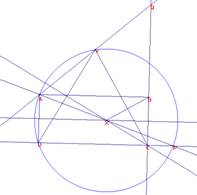
Es reseñable los hechos geométricos siguientes:
1)El centro de la segunda circunferencia, V, pertenece a la primera.
Además XVP es equilátero. De ello se deduce que
2)X, centro de la primera, pertenece a la segunda.
3) Las dos circunferencias tratadas tienen el mismo radio y son simétricas respecto a PY.
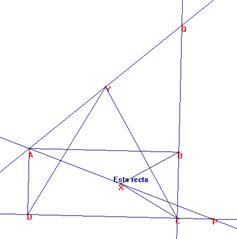
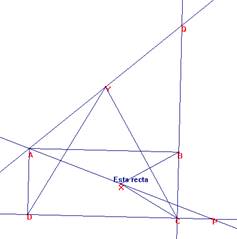
Tomemos origen de coordenadas en D(0,0). Sea A(o,a), C(c,0) y B(c,a).
. 
.
De donde se deduce que el punto 
.
.
.Así, cqd, APQ es un triángulo equilátero.
Ricardo Barroso Campos. Jubilado.
