Problema 664

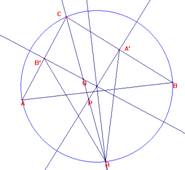
Sea ABC un triángulo y consideremos la bisectriz de C, que corta en R a la circunferencia circunscrita. Las mediatrices de los lados a y b cortan a la bisectriz dada en P y Q. Sean A’ y B’ los puntos medios de los lados BC y AC. Demostrar que las áreas de los triángulos PA’R y QB’R son iguales. 

Jay Warendorff (2012): http://demonstrations.wolfram.com/TwoTrianglesOfEqualAreaOnEitherSideOfAnAngleBisector/

Solución del director

Si a=b, al ser ABC isósceles, es inmediato que las áreas son iguales. Supongamos que a>b. Hagamos la simetría del triángulo QB`R sobre la recta bisectriz CR. La transformada del segmento QR es QR y  B’ se transforma en B’’ sobre CB por ser CR bisectriz.

Deseamos mostrar que

[B’RQ]=[A’RP].

Es [B’’RQ]=[B’RQ] por la construcción hecha.

Luego debemos observar que [B’’RQ]=[A’RP].

Si observamos el cuadrilátero B’’A’RQ, que contiene a los dos triángulos estudiados, lo que habremos de investigar es si las áreas de B’’A’QP y B’’A’ R coinciden, ya que

[A’RP]+[B’’A’QP]= [B’’A’RQ]

[B’’RQ]+[B’’A’R]=  [B’’A’RQ]

Veamos ambas áreas.

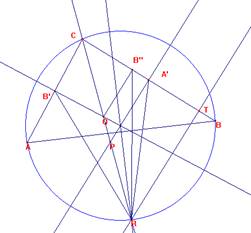
[B’’A’QP]= [CA’P] - [CB’’Q]

CA’P es rectángulo en A’.

CA’=a/2, y A’P= (a/2)tg (γ/2), siendo γ el ángulo ACB.

Así   [CA’P]=(a²/4) tg (γ/2)

De manera análoga, en el triángulo CB’’Q es:

CB’’=b/2, B’’Q=(b/2) tg (γ/2).

Así es  [CB’’Q]=(b²/4) tg (γ/2)

Y [B’’A’QP]= [CA’P] - [C B’’Q]= tg (γ/2) ((a²/4)-(b²/4))

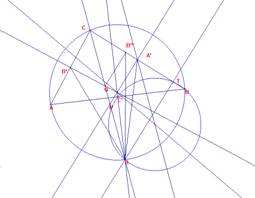
Por otra parte, estudiemos el área del triángulo B’’A’R.

Tomemos como base el lado B’’A’.

La altura será RT, con RT perpendicular sobre CB.

 B’’A’=CA’-CB’’=  a/2 - b/2.

Sea C’ el punto medio de AB.

El cuadrilátero RC’TB es concíclico, pues <RC’B=<RTB=90º.

Por ello <C’TB=180-<C’RB.

<C’RB=1/2<ARB=1/2 (180-<ACB)=90- γ/2

Es decir, <C’TB=180-<C’RB= 180 –(90- γ/2)= 90+ γ/2.

De donde <C’TA’= 180 - <C’TB= 180 – (90 + γ/2)=90-γ/2.

Así el triángulo C’A’T es isósceles, y por ello A’T=A’C’= CA/2=b/2.

De todo lo anterior deducimos que la altura RT del triángulo B’’A’R, teniendo en cuenta el triángulo rectángulo ART, es RT=CT tg (<TCR)= (CA’+A’T )tg (γ/2)= (a/2 + b/2) tg (γ/2) [B’’A’R]= (a/2- b/2) (a/2 + b/2) tg (γ/2). Así pues al ser [B’’A’QP]=[B’’A’R], se obtiene lo pedido.

Ricardo Barroso Campos. Jubilado.