Problema 667

E.2.25 Demostrar que existe una infinidad de triángulos inscritos en una circunferencia de centro O que tienen el mismo ortocentro H, el mismo centro de gravedad G y la misma circunferencia de Euler. (p. 185)

Ladegaillerie, Y. (2005): Geometrie exercises corrigés pour le Capes de mathématiques. Editions Ellipses.

Solución del director.

Caso I):

Sea ABC un triángulo acutángulo. Sea Σ la circunferencia circunscrita de centro  O  y sea Ω la circunferencia de  Euler de ABC de centro N.

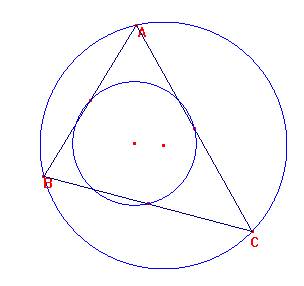
Sea U un punto cualquiera de Σ.  Tracemos la circunferencia Λ de diámetro UO.

Cortará a Ω en dos puntos W y Z.

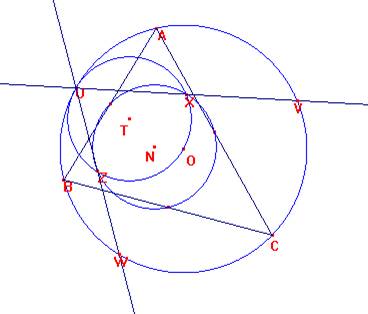
Sean W y V los cortes de las rectas UZ y UX con Σ.

Veamos que el triángulo UVW es uno de los pedidos.

1.- La circunferencia circunscrita a UVW es  Σ   por la construcción de los tres puntos.

2.- U es centro de homotecia de razón ½ que transforma Σ en Λ, por lo que UX=1/2 UV, y

UZ=1/2 UW.  Si observamos la homotecia de centro V y razón ½, de nuevo tendríamos X e Y  tal que VX=1/2 VU y VY=1/2 CW*.

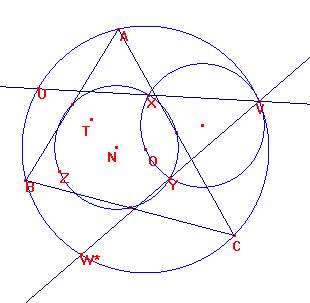
Observando  los triángulos semejantes según las homotecias dadas, UXZ y UVW, por una parte , y por otra VXY y VUW*, los triángulos WZY y W*ZY han de coincidir, por lo que W=W*.

Al ser XYZ los puntos medios de UV, VW y WU, las circunferencias de Euler de ABC y de UVW coinciden, así como N, centro de la misma.

3.- N y O son puntos de la recta de  Euler, por lo que H, ortocentro, no sólo está en este caso en la misma recta, sino que coincide en ambos triángulos estudiados pues es conocido que  d(OH)= 2d(ON).

4.- El centro de gravedad pertenece  a la recta de Euler y es d(G ,H)=2D(G,O)

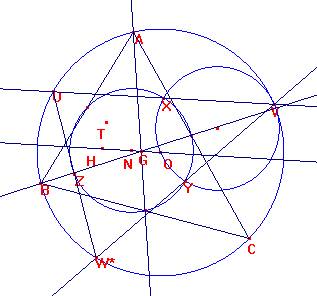
Así pues, cqd también coinciden.

El punto de partida de la construcción, U, puede ser cualquiera de la Σ   por lo que hay infinitos triángulos.

Caso II)

Sea ABC un triángulo rectángulo en C.

Son posibles todos los puntos de Σ, salvo C*, diametralmente opuesto a C.

El triángulo UVW es tal que V=C, y V es diagonalmente opuesto a U.

Caso III)

 Sea ABC obtusángulo con C obtuso.

Tracemos Σ

Tracemos la circunferencia Euler Λ de ABC, cuyo centro es N.

Tracemos la circunferencia Θ de centro O y radio R/2.

Tracemos con centro N la circunferencia Φ de radio 2R.

Sean Q y S los puntos de intersección de Θ y Φ.

Tracemos las dos circunferencias de centros Q y S y radio R/2.

Sean U* y U** los puntos de tangencia de las mismas con Σ.

Tomemos un punto U en el arco [U* U**] que comprende a C.

El triángulo UVW construido de la manera análoga al caso acutángulo es solución del problema.

Ricardo Barroso Campos.

Jubilado