Problema 669

24.- Problema . Se da una circunferencia C y tres diámetros A₁, A₂ y A₃. Construir un triángulo inscrito en C tal que tenga a A₁, A₂ y A₃  como mediatrices.

Azis El Kacimi Alaoui (2012): Geometría euclídea elemental. (p. 79)

Solució de Ricard Peiró:

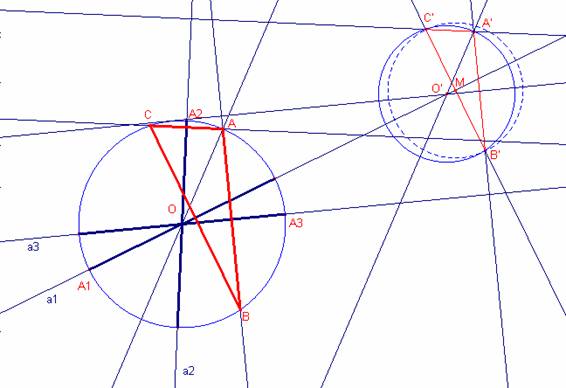
Sea O el circuncentro del triángulo que buscamos.

Los lados del triángulo son perpendiculares a las mediatrices.

Sean las rectas que contienen las mediatrices.

a) Dibujar la recta perpendicular a en un punto cualquiera M de la recta.

b) Dibujar dos puntos B’, C’ que estén a la misma distancia de M en la recta perpendicular anterior.

c) Dibujar la recta perpendicular a que pasa por C’

d) Dibujar la recta perpendicular a que pasa por B’.

e) Les rectas anterior es tallen en el punto A’.

f) El triángulo es semejante al que buscamos.

g) Dibujar el circuncentro O’ del triángulo .

h) Dibujar la recta .

i) Trazar una recta paralela a O’A’ que pase por O.

j) El punto A es la intersección de la recta de l’apartat i) con la circunferencia inicial.

k) Dibujar AB paralelo a A’B’

l) dibujar AC paralelo a A’C’.

Solución con Cabri:

Figura barroso669.fig

Applet created on 17/01/13 by Ricard Peiró with CabriJava