PROBLEMA 671

2.(a) ¿Es posible dividir un triángulo equilátero en 4 triángulos equiláteros?

(b) ¿Es posible dividir un triángulo equilátero en 5 triángulos equiláteros?

(c) Demostrar que cualquier triángulo equilátero se puede dividir en n triángulos equiláteros, para cualquier n>5.

Solución de Inocencio Esquivel García, docente de Matemáticas del Instituto Técnico Patios Centro No. 2 Los Patios N.S. Colombia.

(a) 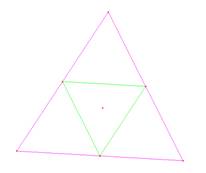Si es posible hacerlo. Desde los puntos medios de cada lado. (fig. 1)

Fig 1

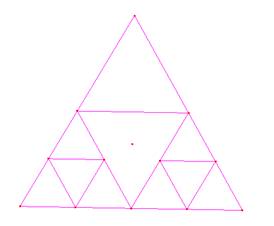
(b) No es posible dividirlo

Cómo se puede ver en las divisiones del inciso (c), cada vértice hace parte de algún triángulo equilátero. Podemos pensar solo en mover uno de los segmentos que une puntos medios y quedaría algo como (Fig. 1b), llevamos 3 triángulos y la figura del centro no puede dividirse en 2 triángulos equiláteros.

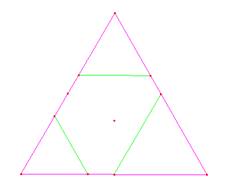
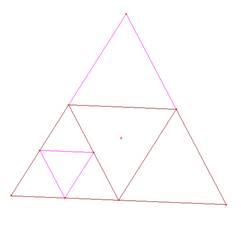
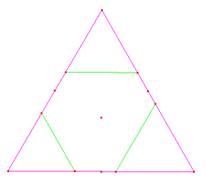Situación aún más difícil si se corrieran dos segmentos que unen puntos medios o los tres. (Fig. 1c) (Fig. 1d)

		Fig. 1d
Fig. 1b	Fig. 1c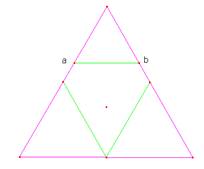

(c) 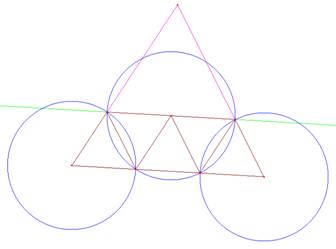Para esta demostración primero se puede construir en el trapecio formado por el segmento paralelo a un lado y que pasa por el circuncentro del triángulo, 5 triángulos equiláteros (iguales) (Fig. 3) y en el trapecio formado por el lado del triángulo y el segmento que pasa por el punto un cuarto del lado del triángulo, 7 triángulos equiláteros (además iguales) (Fig. 4)

	Fig. 3
Fig. 2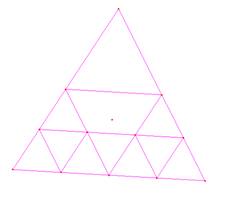

Para dividirlo en 7 ó 10 triángulos tenemos las siguientes figuras (Fig. 4), (Fig. 5)

Fig. 4

Fig. 5

Para n > 5, tomamos la siguiente forma: 5n + 1, 5n + 2, 5n + 3, 5n + 4, 5n (n>1)

y de cada una se hace la construcción.

1. Para Dividir en 5n + 1 triángulos equiláteros

Construimos n trapecios que los dividimos en 5 triángulos más el triángulo que sobra.

2. Para Dividir en 5n + 2 triángulos equiláteros, construimos n – 1 trapecios de 5 triángulos y el triángulo sobrante en 7 triángulos.

3. Para Dividir en 5n + 3 triángulos equiláteros, construimos (n – 1) trapecios de 5 triángulos equiláteros, un trapecio de 7 triángulos equiláteros, más el triángulo que sobra.

4. Para Dividir en 5n + 4 triángulos equiláteros, construimos n trapecios de 5 triángulos equiláteros y el triángulo que sobra lo dividimos en 4 triángulos equiláteros.

5. Para Dividir en 5n triángulos equiláteros, (n > 2), construimos 2 trapecios de 7 triángulos equiláteros y (n – 3) trapecios de 5 triángulos equiláteros más el triángulo que sobra.

Demostrando así que para cualquier n>5 es posible dividir un triángulo equilátero en n triángulos equiláteros