Donat el triangle  determineu les circumferències  tal que  interiors al triangle i que siguen tangents als costats que formen els angles  del triangle i la circumferència k tangent exterior a les altres tres i totes quatre d’igual radi.

Solució:

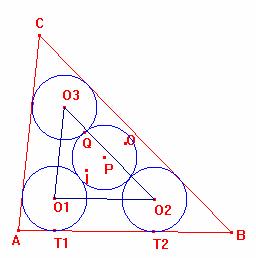
Siguen  els centres de les circumferències  i  el radi.

Considerem el triangle .

Els triangles ,  són semblants.

Siga P el centre de la circumferència k tangent exterior a les circumferències

P és el circumcentre del triangle . El radi de la circumferència circumscrita és 2x.

Aplicant raons trigonomètriques al triangle rectangle : .

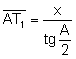Aplicant raons trigonomètriques al triangle rectangle : ..

.

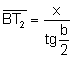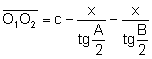Aplicant el teorema dels sinus al triangle :

.

.

 

 

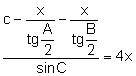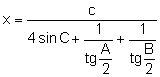Simplifiquem el resultat.

Siguen R, r els radis de les circumferències circumscrita i inscrita al triangle .

Siga  el semiperímetre.

, , .

Solució amb Cabri:

 

 

Figura barroso685.fig

Applet created on 5/06/13 by Administrador with CabriJava