Problema 685

Ejemplo 93. Te dan un triángulo  Construir cuatro circunferencias , de modo que sea verdadero:

1. Las circunferencias   forman parte del triángulo siendo tangentes a los ángulos .

2.- La circunferencia k es tangente exterior a las otras  tres, teniendo todas el mismo radioo.

Kuřina, F (1989) Arte de ver matemática. Statni pedagogiké nakladatelstvi. Praha. (p. 192)

Solución de Ricard Peiró:

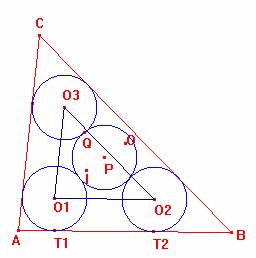
Sean  los centros de las circunferencias  i  el radio.

Consideremos el triángulo .

Los triángulos ,  son semejantes.

Sea P el centro de la circunferencia k tangente exterior a las circunferencias

P es el circuncentro del triángulo . El radio de la circunferencia circunscrita es 2x.

Aplicando razones trigonométricas al triángulo rectángulo : .

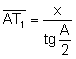Aplicando razones trigonométricas al triángulo rectángulo : ..

.

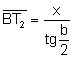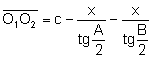Aplicando el teorema de los senos al triángulo :

.

.

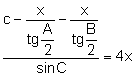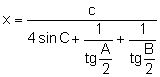Simplifiquemos el resultado.

Sean R, r los radios de las circunferencias circunscrita e inscrita al triángulo .

Sea  el semiperímetro.

, , .

Solución con Cabri:

Figura barroso685.fig

Applet created on 5/06/13 by Ricard Peiró with CabriJava