Problema 686
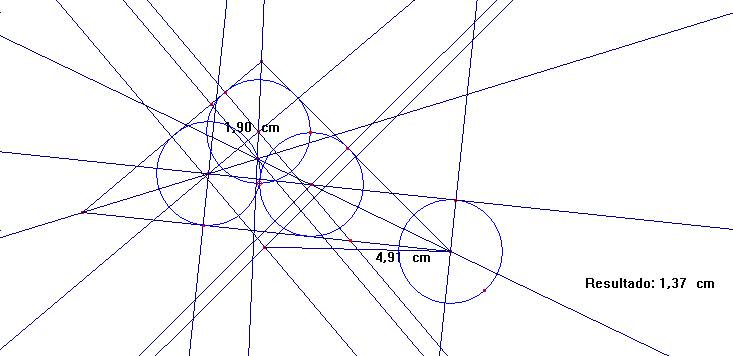
Dado un triángulo ABC,construir tres circunferencias k1 , k2 y k3, del mismo radio, de modo que sean tangentes interiores a los ángulos α , β y γ, y tengan un punto común a las tres.
Barroso, R. (2013): Comunicación personal.
Solución del director.
Supongamos el problema resuelto.
Sea R el circunradio y sea r el inradio de ABC.
Sean O1, O2, y O3 los centros de k1 k2 y k3. O1 O2 O3 habrá de ser semejante a ABC. Sea F el circuncentro de k.
Al ser FO3=FO2=FO1=s, este es el radio circunscrito de O1 O2 O3.
El incentro de O1, O2, y O3 coincide con el de ABC, así, el inradio de O1 O2 O3 es r-s.
Por tanto los correspondientes radios habrán de ser semejantes.
![]() . Es decir,
. Es decir, ![]()
Ricardo Barroso Campos
Jubilado.
Sevilla