Problema 686
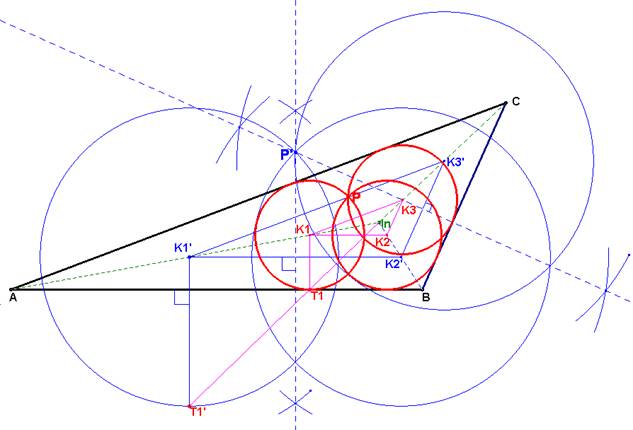
Dado un triángulo ABC,construir tres circunferencias k1 , k2 y k3, del mismo radio, de modo que sean tangentes interiores a los ángulos α , β y γ, y tengan un punto común “P” a las tres.
Barroso, R. (2013): Comunicación personal.
Resuelto por JULIÁN SANTAMARÍA TOBAR profesor de Dibujo del IES
 El
triángulo formado por los centros solución K1 K2 K3 es homotético al triángulo
dado ABC por tener los lados paralelos. El centro de homotecia es el incentro
In del triángulo ABC.
El
triángulo formado por los centros solución K1 K2 K3 es homotético al triángulo
dado ABC por tener los lados paralelos. El centro de homotecia es el incentro
In del triángulo ABC.
El punto común P de las tres circunferencias solución es el circuncentro del triángulo K1 K2 K3 por equidistar de estos centros.
Para resolver el problema se toma un punto cualquiera K1’ en la bisectriz CAB y se completa el triángulo K1’ K2’ K3’ homotético al ABC cuyo centro de homotecia sea el incentro In. Se halla el circuncentro P’ del triángulo K1’ K2’ K3’ por donde pasan las circunferencias homotéticas a la solución. Para obtener la relación de homotecia entre el dibujo auxiliar y la solución se aplica propiedad de tangencia del punto T1 al lado AB.