Propuesto por Miguel-Ángel Pérez García-Ortega, profesor de Matemáticas en el IES "Bartolomé-José Gallardo" de Campanario (Badajoz)
Problema 1002

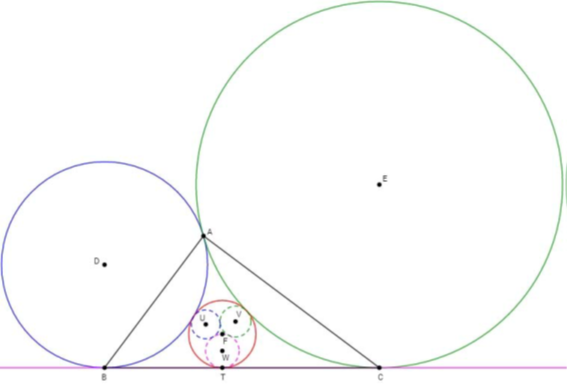
A) Para un triángulo ABC, se consideran las circunferencias que pasan por el punto A y son tangentes a la recta BC en los puntos B y C, respectivamente. Dado un segmento BC, determinar el lugar geométrico que debe describir el punto A para que ambas circunferencias sean tangentes en este punto y, en este caso, determinar el radio de la circunferencia que es tangente a ambas circunferencias y a la recta BC.
B) Dado un triángulo ABC tal que las circunferencias (D) y (E) que pasan por el punto A y son tangentesa la recta BC en los puntos B y C, respectivamente, son tangentes en el punto A, se considera lacircunferencia (F) inscrita en el triángulo mixtilíneo formado por ambas circunferencias y la recta BC.La inversión con respecto a la circunferencia (F)transforma la circunferencia (D) en la circunferencia(U), la circunferencia (E) en la circunferencia (V) y la recta BC en la circunferencia (W). Calcular, enfunción de las longitudes y los radios de las circunferencias (U), (V) y (W)

Pérez M. A. (2021): Comunicación personal.