Propuesto por  César Beade Franco, profesor de matemáticas jubilado de Cee (La Coruña)

Problema 991

Los puntos P, Q, R y S constituyen un sistema ortocéntrico. Determinar un triángulo ABC tal que los 4 puntos P, Q, R, S 
a) Sean los incentros de ABC.
b) Sean los puntos de Nagel de ABC.
c) Sean los puntos de Spieker de ABC.

Beade, C.(2021): Comunicación personal

Aclaración de César Beade

Gergonne, Nagel, Spieker.

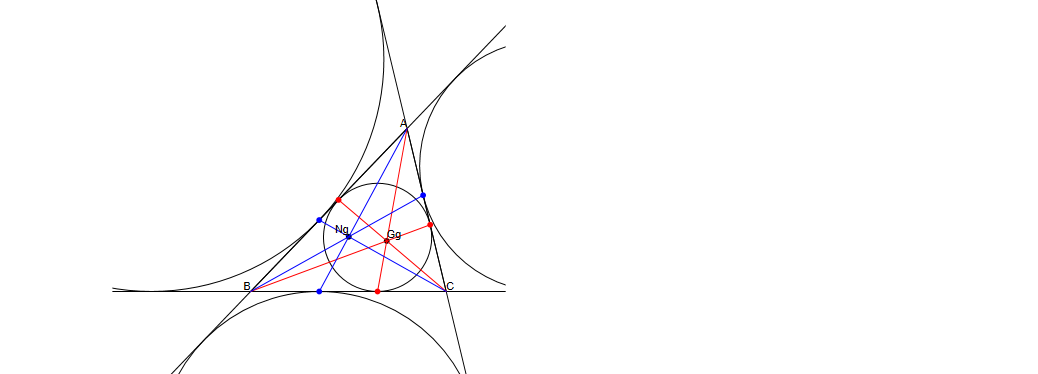
Si unimos cada proyección (en rojo) del incentro sobre un lado con su vértice opuesto obtenemos 3 segmentos que se cortan en el punto de Gergonne, Gg.Si consideramos las proyecciones de los otros incentros (en azul), simétricas de las anteriores respecto a los punto medios de cada lado obtenemos otros 3 segmentos que se cortan en el punto de Nagel, Ng. De su construcción se deduce que Ng es el transformado isotómico de Gg (y viceversa).

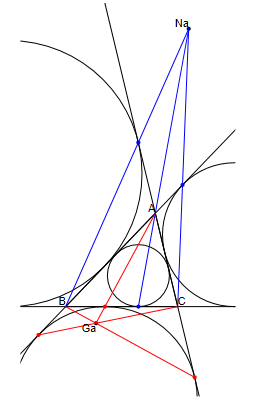
Extendiendo esta construcción a los otros incentros obtenemos sus correspondientes puntos de Gergonne, GgA, GgB y GgC.Sus transformados isotómicos son los otros puntos de Nagel, NgA, NgB y NgC.En el próximo dibujo se muestran GgA y NgA.

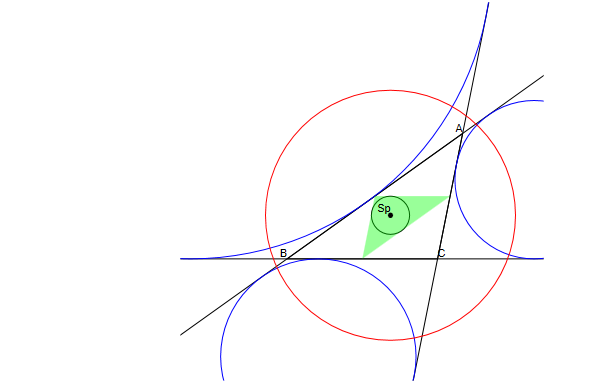
Consideremos ahora los 3 ex-incírculos. Hay una circunferencia que los corta ortogonalmente, su circunferencia de Monge.Su centro es el punto de Spieker, Sp, que no es otro que el incentro del triángulo media

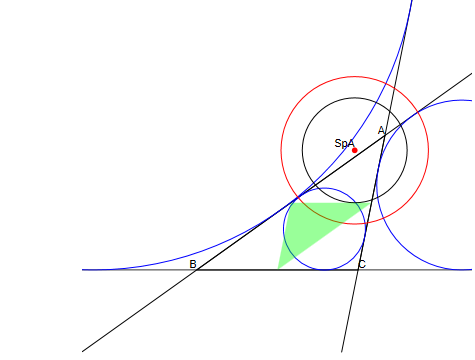
Considerando todos los incírculos y agrupándolos de 3 en 3 obtenemos otras circunferencias de Monge, 4 en total, con sus correspondientes centros o puntos de Spieker, los 4 incentros del triángulo medial.

Los 4 puntos de Ng y los 4 de Sp constituyen sendos sistemas ortocéntricos (íntimamente relacionados)