“...Kepler escribía líricamente: “La Geometría tiene dos grandes tesoros: uno de ellos es el Teorema de Pitágoras; el otro, la división de un segmento en media y extrema razón. El primero lo podemos comparar a una medida de oro; el segundo lo podríamos considerar como una preciosa joya...” (1)

Demostración número veintinueve. (Demostraciones algebraicas)(2)

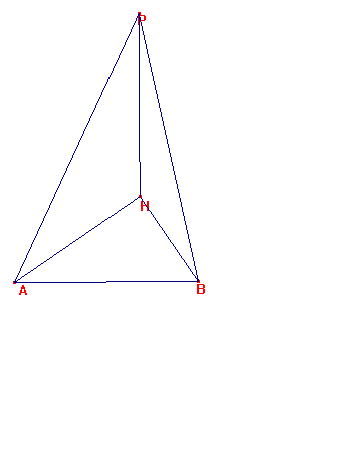
Sea el triángulo AHB con ángulo recto en H. Tracemos por H una perpendicular a AB, tomando en ella PH = AB. Consideremos el área del cuadrilatero AHBP descompuesto en dos triángulos APH y BPH. Se obtiene el teorema según consideremos PH como bases de los dos triángulos o BH y AH como bases.

demostración ciento ochenta y nueve. (Demostraciones geométricas)(2)

La figura se construye con el cuadrado sobre la hipotenusa “hacia dentro del triángulo rectángulo(ABKC)” y los cuadrados de los catetos “hacia dentro del triángulo con vértice en H (HBDE) y a partir de E (ELGF)”.....

(1) Boyer, C. (1.968): A History of Mathematics. Joh Wiley & Sons. Traducción española enn Alianza Universidad Textos. Alianza Editorial Textos (1.987). (pp. 81)

(2)Loomis, E. S. (1.968): The Pythagorean Proposition NCTM Washington D.C. (pp.47, 206)

(contiene 370 demostraciones diferentes del Teorema)

(las observaciones para comprender las figuras son elaboración propia)