Reflejemos el incentro I sobre cada uno de los lados del triángulo, llamando A' (opuesto de A), etc..

Dibujemos las líneas AA', BB', CC'.

Mostrar que:

1.- Estas tres líneas son concurrentes (en un punto J)

2.- El segmento IJ es paralelo a la recta de Euler.

Gray, S. (2.001): Math Forum.

Una cúbica circular en la que se contienen algunos puntos notables del triángulo

Por

François Rideau, Maitre de Conférences à l'Université de Paris 7 (Traducción libre: Ricardo Barroso),

1 Introducción

Sea ABC un triángulo del plano afin euclidiano. Se trata de encontrar el lugar de los puntos P del plano tales que si A’, B’, C’ designan el simétrico respectivos de P con relación a los lados BC, CA, AB entonces las rectas AA’, BB’, CC’ estén vinculadas es decir, sean convergentes o paralelas.

La respuesta a esta cuestión está dada por la serie de teoremas siguientes:

Teorema 1: Si el triángulo ABC es cualquiera es decir, de manera que si el grupo de isométrías que lo conserva se reduce a la aplicación idéntica o de manera más prosaica si el triángulo ABC no es isósceles, entonces el lugar buscado es una cúbica circular (I) que contiene:

- Los tres vértices A, B, C del triángulo.

- El simétrico L de A con relación a BC, el simétrico M de B con relación a CA, el simétrico N de C con relación a AB.

- El ortocentro H.

- El centro del círculo circunscrito O.

- El centro del círculo inscrito I y los 3 centros I_A, I_B, I_C de los círculos exinscritos.

- Los 6 vértices de los triángulos denominados de Napoleón, triángulos equiláteros construidos sobre cada lado del triángulo.

- La dirección asintótica real de la cúbica (I) es la de la recta de Euler del triángulo

Se conocen pues de (I) 18 puntos diferentes a distancia finita además de sus 3 puntos del infinito.

Teorema 2 Si el triángulo ABC es isósceles sin ser equilátero, es decir, si el grupo de isometrías que lo conserva es de orden 2, (por ejemplo AB = AC ≠ BC), la cúbica (I) degenera en la unión de una recta, a saber el eje de simetría del triángulo en este caso aquí la mediatriz de BC y el círculo de centro A que pasa por B y C.

Teorema 3 Si el triángulo ABC es equilátero, (es decir, el grupo de isometrías conservándolo es de orden 6), ¡el lugar es todo el plano!

Nos interesaremos en primer lugar por el teorema 1 y en consecuencia suponer que el triángulo ABC es cualquiera. Se duda lo que es necesario calcular pero no se ve bien muy cómo elegir una señal sin perder el papel simétrico desempeñado por los puntos A, B, C. Hay dos maneras de hacer que conducen más o menos a la misma complejidad de cálculos pero que se complementan bastante bien:

- La utilización de los números complejos que tiene la ventaja de no hacer manejar más que una variable: a saber, el afijo z en vez de dos, la abcisa x y la ordenada y.

- La utilización de las coordenadas baricéntricos con relación al triángulo ABC que tiene la ventaja precisamente de guardar el papel simétrico desempeñado por los vértices A, B, C, aunque los cálculos euclidianos siguen siendo delicados en tal sistema

2 La utilización de los números complejos.

En primer lugar se puede siempre suponer que el plano afín euclideo es el cuerpo C de los complejos provisto de su estructura euclídea normal y que el círculo circunscrito al triángulo ABC es el círculo unidad de los números complejos de módulo 1, lo que va a simplificar mucho el cálculo de las simetrías con relación a los lados del triángulo.

Se podría tomar esta afirmación como verdadera, sin embargo es quizá útil retrasarse.

Prácticamente eso equivale a construir una semejanza:

σ :C → P ; m→ M

Transformando el círculo unidad S¹ de C sobre el círculo circunscrito al triángulo ABC y a identificar todo punto M del plano afín euclídeo P a su afijo m= σ ^-1 (M).

Observemos que por convenio, el afijo de un punto (del plano) definido por una mayúscula se designa por la letra minúscula correspondiente.

Eso es fácil de hacer: La elección de una referencia ortonormal (O;,) permite obtener una isometría:

s: C → P : x + iy → O + x + y

Si h designa una de las 2 homotecias de centro O que transforman el círculo unidad S¹ en el círculo circunscrito al triángulo ABC, entonces σ = h ° s es la semejanza buscada. Se utiliza entonces el siguiente resultado:

Lema 1: Si u y v son 2 complejos de módulo 1, entonces la simetría ortogonal σ con relación a la recta uv está dada por la fórmula:

σ (z)= -uv +u +v

Demostración:

Es claro que σ es una isometría indirecta. Por otra parte

σ (u)= -uv +u +v = u, pues

u = 1,

al ser u de S¹ .

Así mismo σ (v)=v y σ es necesariamente la simetría ortogonal con relación a la recta uv.

c.q.d.

Se desprende de este lema que los simétricos respectivos a’, b’, c’ de z con relación a los lados bc, ca, ab son:

a’ = -bc + b + c , b’ = -ca + c + a c’ = -ab+a + b (1)

Es necesario escribir ahora las ecuaciones de las rectas aa’, bb’, cc’ y para eso se utiliza el siguiente lema:

Lema 2 : Sean u y v 2 complejos distintos. Entonces el complejo Z pertenece a la recta afín uv si y solamente si:

El determinante de orden 3:

(2) 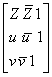=0

Demostración:

Sea σ la simetría ortogonal con relación a la recta uv. Existen dos complejos α y β tales que:

(3) σ (Z)= α + β

Como Z, u y v están fijos por σ, se tiene:

(4) Z = α + β , u = α u + β , v= α + β

Este sistema de 3 ecuaciones de 2 incógnitas a y b es compatible y el determinante de orden 3 de sus coeficientes es pues nulo.

C.q.d.

Se deduce inmediatamente la ecuación de la recta aa’:

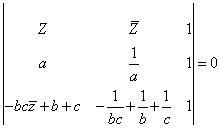
donde se han tenido en cuenta las relaciones:

= 1/a , = 1/b = 1/c

es equivalente a:

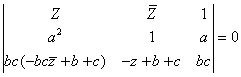
Al desarrollar, se obtiene finalmente la ecuación de aa’:

(5) (bc-ab-ac+az)Z+abc(b+c-a- bc) + ( a ² –bc)(b+c) – a ² z +b² c ² =0

luego por permutación circular sobre a, b, c la de bb’:

(6) (ca-bc-ba+bz)Z+abc(c+a-b-ca )+(b²-ca)(c+a)- b²z+ c² a² =0

y finalmente por una nueva acción de la misma permutación la de cc’:

(7) (ab-ca-cb+cz)Z+abc(a+b-c- ab)+ ( c ² –ab)(a+b) – c ² z +a² b ² =0

Las rectas aa’, bb’, cc’ serán pues concurrentes si el sistema siguiente admite una solución en Z, , es decir, es compatible si y solamente si el determinante de sus coeficientes es nulo:

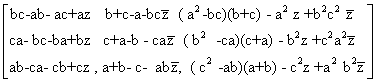=0

Es la ecuación del lugar buscado. Obviamente se tiene el derecho a seguir revelándose ante este determinante que va a ser necesario desarrollarlo incluso aunque sea de grado 3. Pero se pueden hacer las observaciones siguientes:

Please enable Java for an interactive construction (with Cinderella).

- Este determinante es un polinomio de Z [a, b, c, z, ].

- Es antisimétrico en (a, b, c) y en consecuencia divisible por el polinomio de Vandermonde

V (a, b, c)= (a -b) (a -c) (b-c)

Aunque el cálculo de este determinante sigue siendo delicado, se sabe a priori que se simplifica mucho y como estamos en el siglo XXI el autor de estas líneas no vacila, y se le pidió fríamente a Mathematica dividir este determinante por el de Vandermonde V (a, b, c) para obtener el siguiente resultado:

(8)

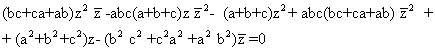
Los términos de mayor grado son:

lo que demuestra que el lugar es una cúbica.

La factorización del término en z muestra que esta cúbica es circular.

La relación de Euler:

OH= 3 OG

Donde G es el baricentro de los puntos A,B , C , muestra que el afijo h del ortocentro es igual a a+b+c.

La ecuación de la recta de Euler es pues:

es decir:

,

o sea:

lo que demuestra que la recta de Euler es la dirección asintótica real de la cúbica.

Queda por comprobar que los puntos a distancia finita citados en el teorema 1 están sobre la cúbica:

Algunos son evidentes geométricamente como los vértices A, B, C y el ortocentro H.

Lo mismo ocurre con los puntos L, M, N. Por ejemplo para el punto L, el simétrico de L_A de L con relación a BC es el punto A teniendo en cuenta el hecho de que todo punto del plano está vinculado afinmente con los puntos A, L_A y está claro que si L_B y L_c designan los simétricos respectivos de L con relación a los lados CA y AB, la intersección de las rectas B L_B y C L_AC ¡están contenidas en el plano! Es evidente también a partir de la ecuación (8) que el centro del círculo circunscrito O de afijo 0 está sobre la cúbica.

De manera general para todos los puntos citados cuyo afijo se calcula `` bien' ', es relativamente fácil ver que estos afijos verifican la ecuación (8). Es el caso de los puntos A, B, C, O, H de afijos a, b, c, 0, a+b+c.

El punto L tiene por afijo l = - [ bc/a]+b+c y se ve que l anula la primera línea del determinante. Se tiene obviamente un razonamiento similar para los puntos M y N con las segundas y terceras líneas.

La situación de los puntos restantes es más delicada.

La de las vértices denominados “de Napoleón” está regulada por el lema siguiente muy conocido:

Lema 3:
si z1,z2,z3 son los afijos de los vértices de un triángulo equilattero, entonces z1 +j.z2+ j^{2}.z3=0
j designa aqui una raiz cúbica de 1, diferente de 1, por ejemplo j=exp[(2.pi.i)/3] o j=exp[-(2.pi.i)/3].
La eleccion del signo (en la expresion de j) corresponde a las 2 orientaciones posibles del triangulo z1,z2,z3.

Se desprende que los afijos de los “vértices de Napoleón” son: ±(jb + j² c), ±(jc + j² a), ±(ja + j² b).

El lector valiente pondrá de manifiesto que estos 6 afijos comprueban la ecuación (8).

El caso de los centros de los círculos inscrito y exinscritos es diferente. La dificultad procede debido a que sus afijos no se expresan racionalmente en función de a, b, c. Se puede extraer siguiendo una idea del famoso Morley, (sí, ¡el del teorema!).

Se eligen raíces cuadradas α, β, γ respectivas de a, b, c de modo que:

a= α² , b = β², c= γ²

Entonces los afijos de los centros de los círculos inscrito y exinscritos están en una permutación:como

β γ + γ α - α β, γ α+ α β- β γ, α β+ β γ - γ α, -( β γ + γ α + α β)

Ya que la elección de los signos de las raíces cuadradas tiene

permuta estos 4 afijos según la teoría de Galois (a un nivel elemental).

El lector valiente pondrá de manifiesto que estos 4 afijos comprueban la ecuación (8).

El lector perezoso puede también utilizar Cabri para comprobar que todos estos puntos están por supuesto sobreel lugar.

El lector motivado puede también buscar una solución geométrica como la que se pide en el problema 39.

Continúa en: 3.- Coordenadas baricéntricas