Problema 43

Doble edición festiva 16 de Diciembre - 31 de Diciembre de 2001

Demostración de la fórmula de Herón:

El área de un triángulo de lados a, b y c, y semiperímetro s es:

Heat, T. (1.921/1.981) A history of Greek Mathematics. Dover Publications; Inc. New York

Solución de Maite Peña Alcaraz, estudiante de Industriales en la Universidad de Comillas (Madrid) (9 de noviembre de 2004)

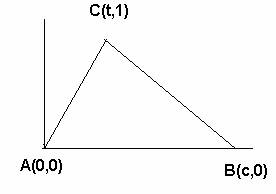
Tomemos un triángulo ABC en los ejes cartesianos:

Así que el área de este triángulo será c/2. Por otro lado sus lados miden:

a²=(c-t)²+1=c²+t²-2ct+1 (Por el Teorema de Pitágoras)

b²=t²+1 (Por el Teorema de Pitágoras)

c²=c²

Calculemos ahora cuanto vale

p(p-a)(p-b)(p-c)=1/2⁴ (a+b+c)(-a+b+c)(a-b+c)(a+b-c)=

½⁴ (-a²+b²+c²+2bc)(a²-b²-c²+2bc)= ½⁴ (-a⁴-b⁴-c⁴+2a²b²+2b²c²+2c²a²)

Y sustituyendo con los valores que tenemos:

½⁴(-c⁴-t⁴-4c²t²-1-2c²t²+2c³t-2ct-2c²-2t²-t⁴-2t²-1-c⁴+2c²t²+2c²+2t⁴+2t²-2ct³-2ct+2t²+2+2c⁴+2c²t²-2c³t+2c²+2c²t²+2c²)

y operando obtenemos:

c²/2² que al sacarle la raíz cuadrada es el área del triángulo.