Sean I1 la involución sobre BC, sección de la involución rectangular de vértice A, análogamente I2, I3 sobre CA,  CB.

Sean L, M y N los pies de las alturas.

Sean M1 sobre CA tal que ABM1 =90º.  N1, N2 sobre B tales que ACN1=BCN2 =90º, y L2 sobre BC tal que BAL2 =90º.

Sea j1 el haz de círculos determinado por el círculo (AM1N1) y la recta MN cuyos puntos base son F1F'1=(AM1N1) ÇMN,

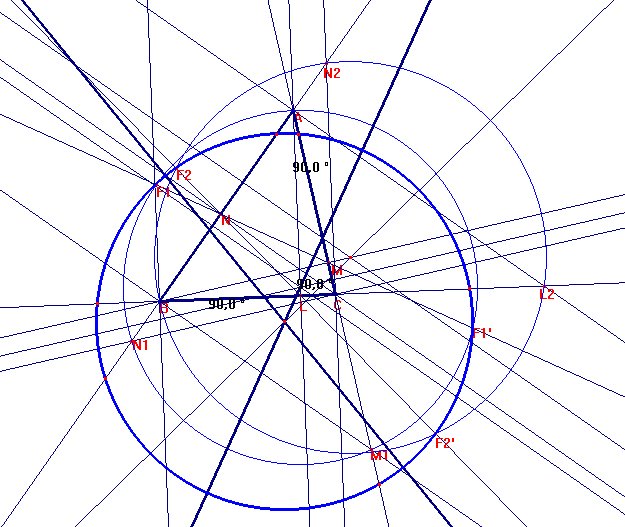
Análogamente el haz  j2 ={(BN2L2), NL} de puntos base F2 F'2.

Los círculos del haz  j1 cortan a los lados CA, AB en pares de puntos de I2, I3 (ya que I2(M)=µ, I2(A)=N, I3(N)= µ, I3(A)=N1), y los círculos de j2 cortan  AB, BC en pares de puntos de I3 I1. El círculo W que pasa por F1, F'1, F2 pasará también por F'2 ya que W corta AB según un par de I3. Luego W es solución del problema.

Barcelona enero  1986 Jordi Dou

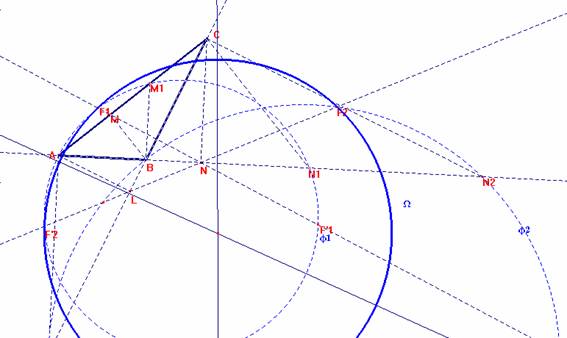
NOTA: los puntos A'A'' B'B'' C'C'' existen siempre (son reales ) y únicos, ya que siendo I2 I3 elípticos, F1 F'1 son reales y "separados" respecto  las rectas CA AB y análogamente F2 F'2 respecto AB, BC