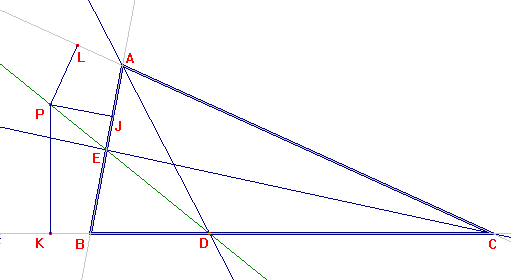
|
Propuesta de Juan Carlos Salazar, Profesor de GeometrÃa del Equipo OlÃmpico de Venezuela.(Puerto Ordaz). Problema 150.- Sea el triángulo ABC,donde AD y CE son bisectrices interiores.En la prolongación
de ED se toma el punto P, desde el cual trazamos las perpendiculares PJ,PK
y PL sobre AB, BC y AC respectivamente. Probar que: PK=PJ+PL. Salazar, J.L. (2004): Comunicación personal. |
Solución del profesor Francisco Javier García Capitán
del IESÁlvarez Cubero (Priego de Córdoba)
La situación se muestra en la siguiente figura:
Usaremos las coordenadas baricéntricas: A=(1,0,0), B=(0,1,0), C=(0,0,1).
Teniendo en cuenta el teorema de la bisectriz, es BD:DC=c:b, por lo que D=(0,b,c). Análogamente es E=(a,b,0). La ecuación en coordenadas baricéntricas de la recta DE es
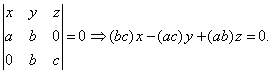
En un punto P como el de la figura, en la prolongación
de DE, las coordenadas baricéntricas son de la forma 
,
por lo que tendremos 
Notas: