Problema 223 de triánguloscabri
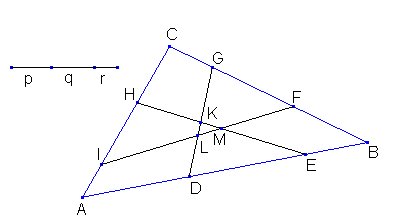
Consideremos un triángulo ABC cualquiera. Sean D y E puntos sobre el lado BC, F y G puntos sobre el lado CA y H y I puntos sobre el lado AB, tal que BD:DE:EC = CF:FG:GA = AH:HI:IB = p:q:r  con p+q+r=1,  p,q, r > 0.Sean K, L y M los puntos de intersección de las diagonales DG y EH, FI y DG, y EH y FI. Probar que :
  1. El área de los cuadriláteros DEFG, FGHI, y HIDE es igual a q veces el área de ABC.
  2. Las áreas de los triángulos GHK, IDL y EFM  son iguales a k -se hallará- veces el área de ABC.
  3. Las áreas de los triángulos DEK, FGL y HIM son iguales a h -se hallará- veces el área de ABC.
  4. El área del triángulo KLM es igial a l -se hallará-, veces al área de ABC.

Gerdes, P. (2003): Dividing the sides of a triangle in proportional parts. Visual Mathematics, Volume 5, No. 2, 2003.
Propuesto por Juan Bosco Romero.

Solución de Francisco Javier García Capitán

Para resolver este problema vamos a usar las coordenadas baricéntricas y el programa Mathematica. Desde aquí puedes ver: