 |
|
Figura
1
|
Comenzamos un poco fuerte, introduciendo la fórmula para la distancia al cuadrado de dos puntos en coordenadas baricéntricas homogéneas.
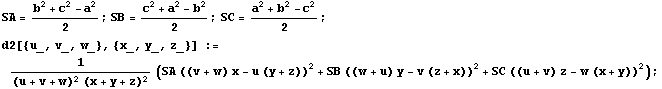
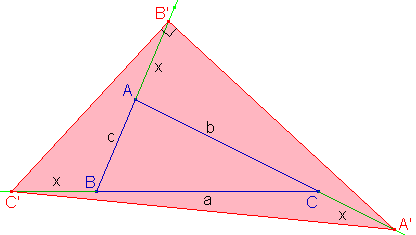
A continuación, introducimos las coordenadas de los puntos A', B', C' en función del número x que queremos determinar.
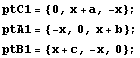
Ahora, imponemos la condición de que el triángulo A'B'C' debe ser rectángulo en B':
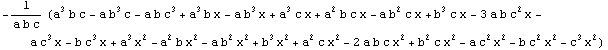
Vemos que se trata de un polinomio de segundo grado. Hallando sus raíces tendremos el valor x buscado.
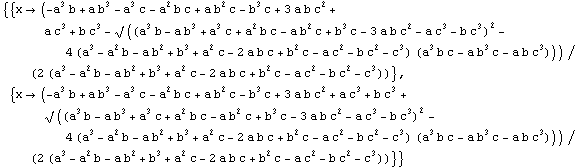
Para poder introducir estas soluciones en la Calculadora de Cabri, necesitamos expresar el resultado de otra forma:
{{x -> (-(a^3*b) + a*b^3 - a^3*c - a^2*b*c + a*b^2*c -
b^3*c + 3*a*b*c^2 + a*c^3 + b*c^3 -
Sqrt[(a^3*b - a*b^3 + a^3*c + a^2*b*c - a*b^2*c
+ b^3*c - 3*a*b*c^2 - a*c^3 - b*c^3)^2 -
4*(a^3 - a^2*b - a*b^2 + b^3 + a^2*c
- 2*a*b*c + b^2*c - a*c^2 - b*c^2 - c^3)*
(a^3*b*c - a*b^3*c - a*b*c^3)])/(2*(a^3
- a^2*b - a*b^2 + b^3 + a^2*c - 2*a*b*c +
b^2*c - a*c^2 - b*c^2 - c^3))},
{x -> (-(a^3*b) + a*b^3 - a^3*c - a^2*b*c + a*b^2*c - b^3*c + 3*a*b*c^2
+ a*c^3 + b*c^3 +
Sqrt[(a^3*b - a*b^3 + a^3*c + a^2*b*c - a*b^2*c
+ b^3*c - 3*a*b*c^2 - a*c^3 - b*c^3)^2 -
4*(a^3 - a^2*b - a*b^2 + b^3 + a^2*c
- 2*a*b*c + b^2*c - a*c^2 - b*c^2 - c^3)*
(a^3*b*c - a*b^3*c - a*b*c^3)])/(2*(a^3
- a^2*b - a*b^2 + b^3 + a^2*c - 2*a*b*c +
b^2*c - a*c^2 - b*c^2 - c^3))}}
Todavía tendremos que hacer algunos arreglos, como sustituir los corchetes por paréntesis, poner todo el texto de una fórmula en una línea para que la Calculadora de Cabri lo acepte. Puede presentarse algún problema adicional si Cabri comete errores de redondeo al efectuar potencias, por lo que es conveniente convertir éstas en productos. Aquí está la expresión de una de las soluciones tal como debemos introducirla en la ventana de la calculadora:
(-(a*a*a*b) + a*b*b*b - a*a*a*c - a*a*b*c + a*b*b*c - b*b*b*c + 3*a*b*c*c + a*c*c*c + b*c*c*c+sqrt((a*a*a*b - a*b*b*b + a*a*a*c + a*a*b*c - a*b*b*c + b*b*b*c - 3*a*b*c*c - a*c*c*c - b*c*c*c)^2 -4*(a*a*a - a*a*b - a*b*b + b*b*b + a*a*c - 2*a*b*c + b*b*c - a*c*c - b*c*c - c*c*c)*(a*a*a*b*c - a*b*b*b*c - a*b*c*c*c)))/(2*(a*a*a - a*a*b - a*b*b + b*b*b + a*a*c - 2*a*b*c +b*b*c - a*c*c - b*c*c - c*c*c))
Habrá, en general, dos soluciones del problema. Cuando se obtengan valores negativos de x, como ocurre para ambas soluciones en la figura siguiente, el triángulo correspondiente estará inscrito en el dado.
 |
|
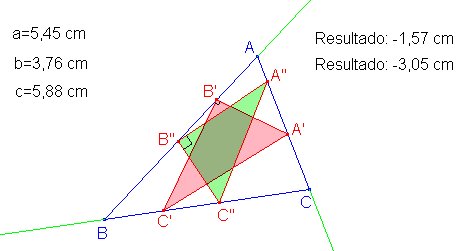Figura
2:
|
Aquí vemos un caso en el que hay una solución positiva y otra negativa:
 |
|
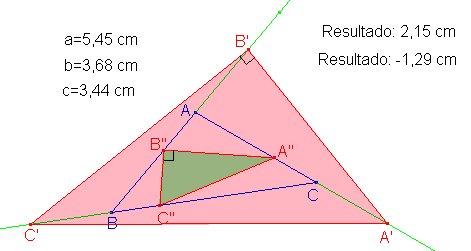Figura
2:
|
Solución en el caso del triángulo rectángulo en A.
En el caso del triángulo rectángulo, los cálculos son mucho más sencillos:
Vemos que una solución siempre es cero. La otra la podemos expresar así:
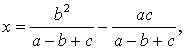
es decir es la diferencia de dos segmentos de la forma 
,
donde u, v y w son conocidos.
Para
construir tales segmentos usaremos una figura como la mostrada a la derecha:
Si las cuerdas AB y CD se cortan en O, entonces OA·OB
= OC·OD, de donde podemos obtener:
Todo lo que tenemos que hacer es aplicar este método dos veces con los valores que aparecen en la fórmula de x. El único de esos valores que no es un lado del triángulo dado es a-b+c = 2·(s-b), el doble doble de la distancia BD, siendo D el punto de contacto de la circunferencia inscrita con BC. Por tanto, la expresión de x puede hallarse fácilmente.
.
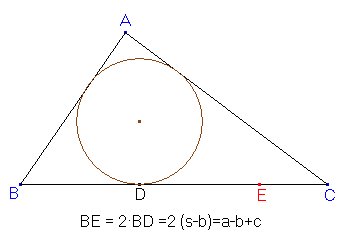
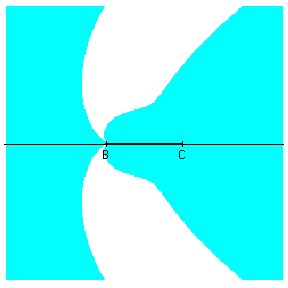
Supongamos que fijamos el segmento BC. Moviendo el punto A vemos que hay solución del problema en algunos casos y no en otros. Evidentemente, estos últimos corresponden a aquellos en los que el radicando de la fórmula de x es negativo.
¿Qué región forman los puntos A para los que hay solución? ¿Cómo hallarla con Cabri?
Hallemos el simétrico A* de A respecto de B' y luego el simétrico A** de A* respecto de B'. El punto A** es lo que Roger Cuppens llama ping-pong central en el capítulo Geometría Lógica de su cuaderno Avec Cabri-Géomètre II, jouez... et faites de la Géomètrie! (tomo II).
Es claro que A** existirá y coincidirá con A si y solo si B' existe, es decir si la construcción es posible.
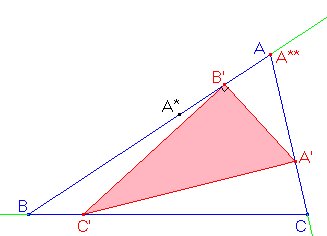
Por tanto, usando la herramienta Traza de Cabri sobre el punto A** y arrastrando A por la pantalla irán apareciendo puntos correspondientes a A para los que el problema tiene solución. El resultado es parecido al siguiente:
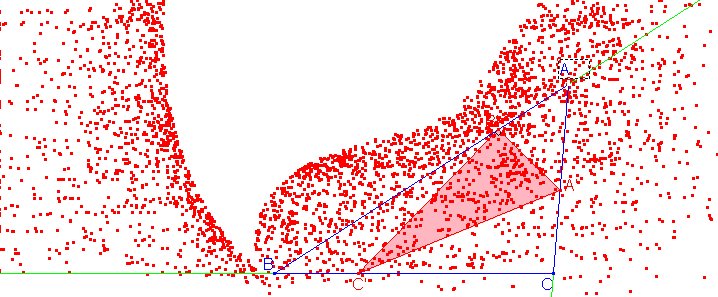
Esta otra figura está obtenida con la ayuda de Mathematica, considerando que B=(-1,0), C=(1,0), variando A y comprobando directamente que la ecuación de segundo grado de la que x es solución tiene discriminante no negativo:
