Problema 232 de triánguloscabri

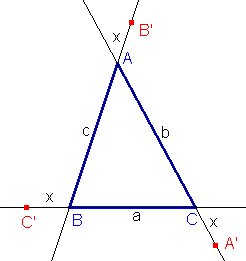
Sea ABC un triángulo isósceles siendo AB=AC. Hallar x real tal que si tomamos a+x, b+x, c+x, prolongando una longitud x a a desde B, y obteniendo C' , prolongando una longitud x a b desde C y obteniendo A', y prolongando una longitud x a c desde A y obteniendo B', el triángulo A'B'C' sea isósceles, siendo B'C' = B'A'.

Propuesto por Juan Bosco Romero Márquez

Solución de Francisco Javier García Capitán

1. Convenio. Consideramos que x es positivo cuando C' se aleja de B en la dirección de la semirrecta CB, y en consonancia, cuando A' se aleja de C en la dirección de AC y B' se aleja de A en la dirección de BA.

Por el contrario, si C' está en la semirrecta BC®, enctonces x será negativo, y A' y B' estarán en las semirrectas CA® y AB®, respectivamente.

Naturalmente, en el el caso x =0 tendremos que B'C'A' es el triángulo dado.

2. Coordenadas baricéntricas. Continuando con la misma figura, e independientemente de que x sea positivo o negativo, se cumple que

Análogamente, tendremos:

3. Cálculos con Mathematica.

Comenzamos introduciendo la fórmula de la distancia entre dos puntos, conocidas sus coordenadas baricéntricas homogéneas. Esta fórmula puede encontrarse en el trabajo Introduction to the Geometry of the Triangle, de Paul Yiu.

Ahora, indicamos que nuestro triángulo es isósceles con AB = AC, introducimos las coordenadas de los los puntos A', B', C', e imponemos que B'A' = B'C':

Nota: Para descargar un cuaderno de Mathematica con éste código, pulsa aquí.

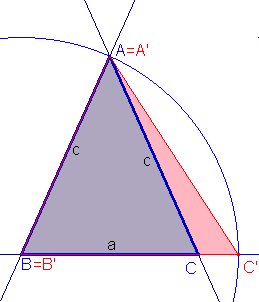
4. Construcción con Cabri. Para hacer una construcción con Cabri de la solución no trivial x = -c, bastará trazar una circunferencia con centro B y radio BA=c, que cortará a la semirrecta BC® en el punto buscado C'. El punto A' estará en la semirrecta CA® con CA'=c, por lo que A=A'. Análogamente, el punto B' estará en la semirrecta AB®, con AB'=c, por lo que B=B'.