Problema 336 de triánguloscabri

En un triangulo ABC, con la notación habitual demostrar que:

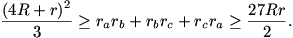
\frac{(4 R+r)^{2}}{3}\geq r_{a}r_{b}+r_{b}r_{c}+r_{c}r_{a}\geq \frac{27Rr}{2}.
Propuesto por José Carlos Chávez Sandoval

Solución de Francisco Javier García Capitán

Usando la identidad 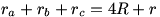r_{a}r_{b}+r_{b}r_{c}+r_{c}r_{a}= 4 R+r, cuya justificación puede verse aquí, la primera desigualdad se convierte en

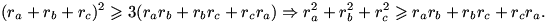
(r_{a}r_{b}+r_{b}r_{c}+r_{c}r_{a})^{2}\geqslant 3(r_{a}r_{b}+r_{b}r_{c}+r_{c}r_{a}) \Rightarrow r_{a}^{2}+r_{b}^{2}+r_{c}^{2}\geqslant r_{a}r_{b}+r_{b}r_{c}+r_{c}r_{a}.

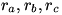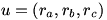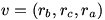Esta desigualdad siempre es cierta incluso para valores negativos de las variables r_{a}, r_{b}, r_{c}, ya que aplicando la desigualdad de Cauchy-Schwarz a los vectores u=(r_{a},r_{b},r_{c}) y v=(r_{b},r_{c},r_{a}) tendremos

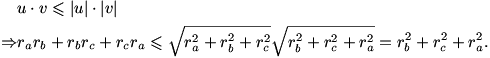
\begin{aligned}& u \cdot v \leqslant \left| u \right| \cdot \left| v \right| \\ \Rightarrow & r_{a}r_{b}+r_{b}r_{c}+r_{c}r_{a}\leqslant \sqrt{r_{a}^{2}+r_{b}^{2}+r_{c}^{2}}\sqrt{r_{b}^{2}+r_{c}^{2}+r_{a}^{2}}= r_{b}^{2}+r_{c}^{2}+r_{a}^{2}. \\ \end{aligned}

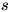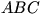Ahora, siendo s el semiperímetro de ABC y multiplicando los valores

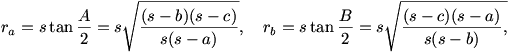
r_{a}= s\tan \frac{A}{2}= s\sqrt{\frac{{(s-b)(s-c)}}{{s(s-a)}}},\quad r_{n}= s\tan \frac{B}{2}= s\sqrt{\frac{{(s-c)(s-a)}}{{s(s-b)}},}

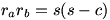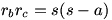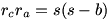obtenemos r_{a}r_{b}= s (s-c), y como de forma análoga es r_{b}r_{c}= s(s-a) y r_{c}r_{a}= s(s-b), tenemos

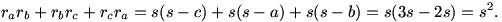
r_{a}r_{b}+r_{b}r_{c}+r_{c}r_{a}= s(s-c)+s(s-a)+s(s-b) = s(3s-2s) = s^{2}.

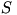Por otro lado, siendo S el área del triángulo ABC, de las fórmulas del área obtenemos

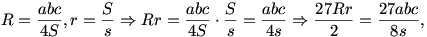
R = \frac{{abc}}{{4S}},r = \frac{S}{s}\Rightarrow Rr = \frac{{abc}}{{4S}}\cdot \frac{S}{s}= \frac{{abc}}{{4s}}\Rightarrow \frac{{27Rr}}{2}= \frac{{27abc}}{{8s}},

por lo que la segunda desigualdad propuesta se escribe

s^{2}\geqslant \frac{{27abc}}{{8s}}\Leftrightarrow 8s^{3}\geqslant 27abc \Leftrightarrow (\frac{{2s}}{3})^{3}\geqslant abc \Leftrightarrow \frac{{a+b+c}}{3}\geqslant \sqrt[3]{{abc}},

que es la conocida desigualdad entre las medias aritmética y geométrica.